| << Chapter < Page | Chapter >> Page > |
Heron’s formula finds the area of oblique triangles in which sides and are known.
where is one half of the perimeter of the triangle, sometimes called the semi-perimeter.
Find the area of the triangle in [link] using Heron’s formula.
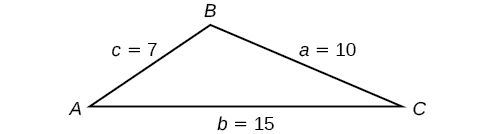
First, we calculate
Then we apply the formula.
The area is approximately 29.4 square units.
Use Heron’s formula to find the area of a triangle with sides of lengths and
Area = 552 square feet
A Chicago city developer wants to construct a building consisting of artist’s lofts on a triangular lot bordered by Rush Street, Wabash Avenue, and Pearson Street. The frontage along Rush Street is approximately 62.4 meters, along Wabash Avenue it is approximately 43.5 meters, and along Pearson Street it is approximately 34.1 meters. How many square meters are available to the developer? See [link] for a view of the city property.
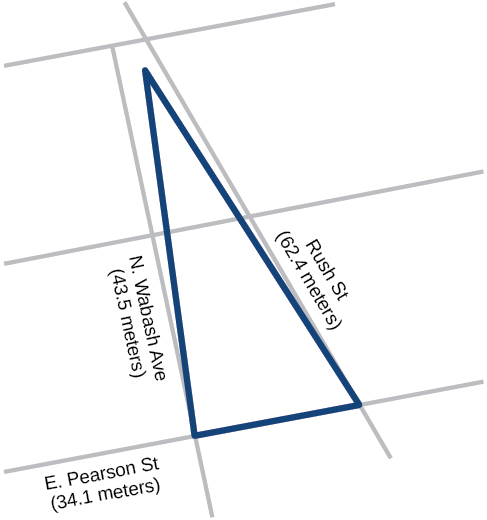
Find the measurement for which is one-half of the perimeter.
Apply Heron’s formula.
The developer has about 711.4 square meters.
Find the area of a triangle given and
about 8.15 square feet
Access these online resources for additional instruction and practice with the Law of Cosines.
| Law of Cosines | |
| Heron’s formula |
If you are looking for a missing side of a triangle, what do you need to know when using the Law of Cosines?
two sides and the angle opposite the missing side.
If you are looking for a missing angle of a triangle, what do you need to know when using the Law of Cosines?
Explain what represents in Heron’s formula.
is the semi-perimeter, which is half the perimeter of the triangle.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?