| << Chapter < Page | Chapter >> Page > |
Find the x -intercepts of
We can attempt to factor this polynomial to find solutions for
This gives us five x -intercepts: and See [link] . We can see that this is an even function because it is symmetric about the y -axis.
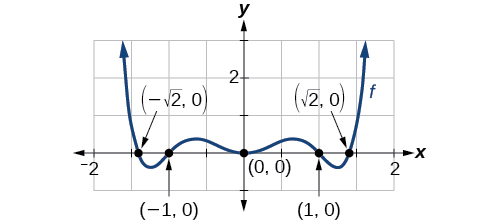
Find the x -intercepts of
Find the y - and x -intercepts of
The y -intercept can be found by evaluating
So the y -intercept is
The x -intercepts can be found by solving
So the x -intercepts are and
Find the x -intercepts of
This polynomial is not in factored form, has no common factors, and does not appear to be factorable using techniques previously discussed. Fortunately, we can use technology to find the intercepts. Keep in mind that some values make graphing difficult by hand. In these cases, we can take advantage of graphing utilities.
Looking at the graph of this function, as shown in [link] , it appears that there are x -intercepts at and
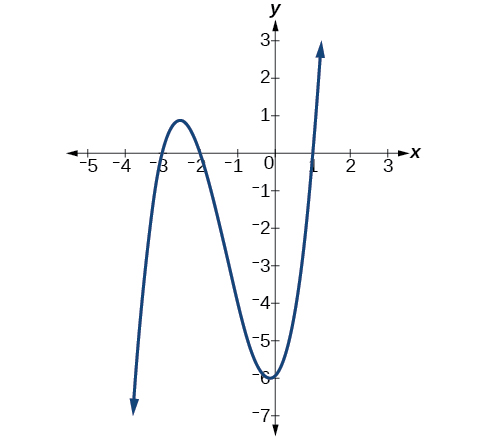
We can check whether these are correct by substituting these values for and verifying that
Since we have:
Each x -intercept corresponds to a zero of the polynomial function and each zero yields a factor, so we can now write the polynomial in factored form.
Find the y - and x -intercepts of the function
y -intercept x -intercepts and
Graphs behave differently at various x -intercepts. Sometimes, the graph will cross over the horizontal axis at an intercept. Other times, the graph will touch the horizontal axis and "bounce" off.
Suppose, for example, we graph the function shown.
Notice in [link] that the behavior of the function at each of the x -intercepts is different.
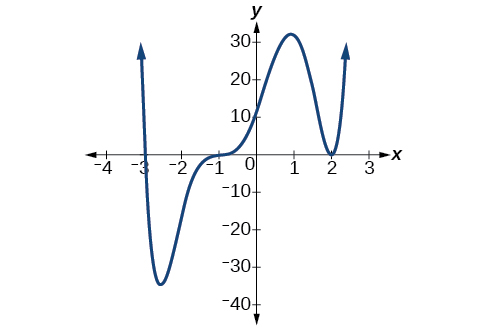
The x -intercept is the solution of equation The graph passes directly through the x -intercept at The factor is linear (has a degree of 1), so the behavior near the intercept is like that of a line—it passes directly through the intercept. We call this a single zero because the zero corresponds to a single factor of the function.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?