| << Chapter < Page | Chapter >> Page > |
Represent the following on number lines:
A linear inequality is similar to a linear equation in that the largest exponent of a variable is 1. The following are examples of linear inequalities.
The methods used to solve linear inequalities are identical to those used to solve linear equations. The only difference occurs when there is amultiplication or a division that involves a minus sign. For example, we know that . If both sides of the inequality are divided by , is not greater than . Therefore, the inequality must switch around, making .
For example, if , then .
In order to compare an inequality to a normal equation, we shall solve an equation first. Solve .
If we represent this answer on a number line, we get
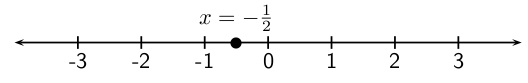
Now let us solve the inequality .
If we represent this answer on a number line, we get

As you can see, for the equation, there is only a single value of for which the equation is true. However, for the inequality, there is a range of values for which the inequality is true. This is the main difference between an equation and an inequality.
Khan academy video on inequalities - 1
Khan academy video on inequalities - 2
Solve for :
When you multiply by a minus sign, the direction of the inequality changes.
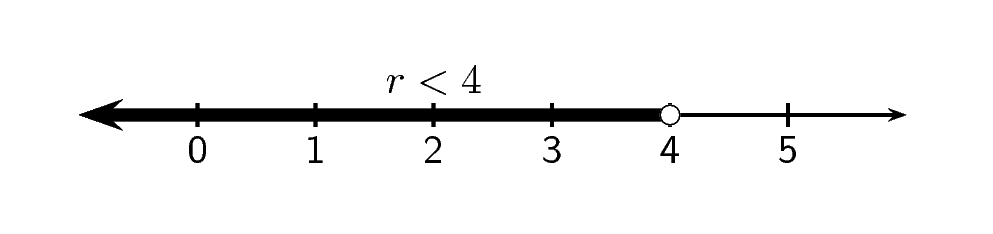
Solve for : and represent the solution on a number line.
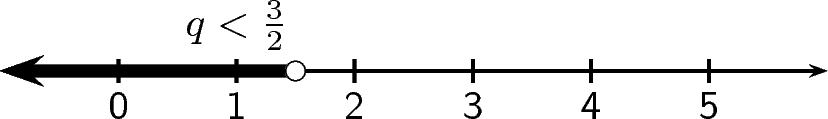
Solve for : and represent solution on a number line.
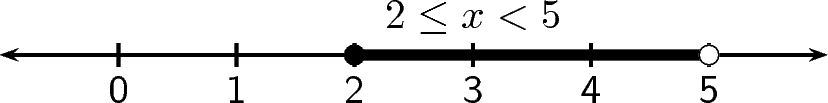

Notification Switch
Would you like to follow the 'Maths grade 10 rought draft' conversation and receive update notifications?