| << Chapter < Page | Chapter >> Page > |
From the Pythagorean Theorem, we get
Substituting we get
Solving for we get
Since has the terminal side in quadrant I where the y- coordinate is positive, we choose the positive value.
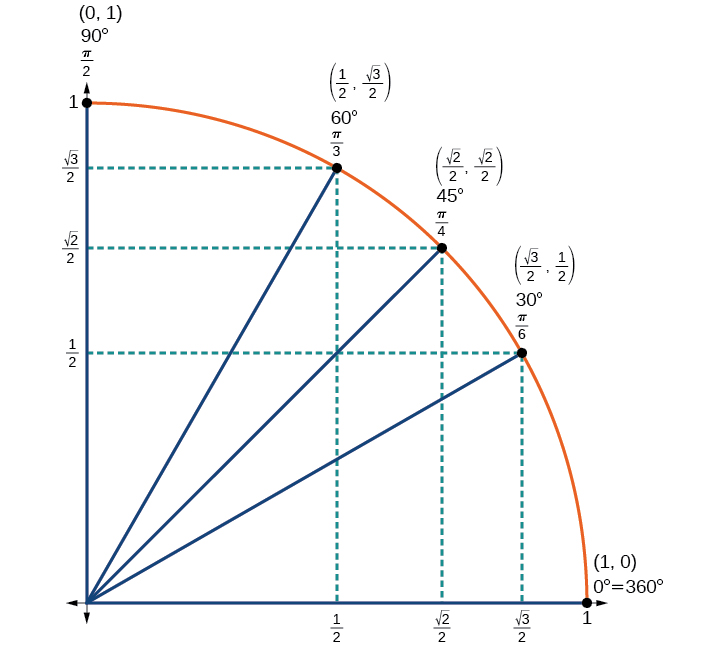
At (60°), the coordinates for the point on a circle of radius at an angle of are so we can find the sine and cosine.
We have now found the cosine and sine values for all of the most commonly encountered angles in the first quadrant of the unit circle. [link] summarizes these values.
| Angle | or | or | or | or | |
| Cosine | 1 | 0 | |||
| Sine | 0 | 1 |
[link] shows the common angles in the first quadrant of the unit circle.
To find the cosine and sine of angles other than the special angles, we turn to a computer or calculator. Be aware : Most calculators can be set into “degree” or “radian” mode, which tells the calculator the units for the input value. When we evaluate on our calculator, it will evaluate it as the cosine of 30 degrees if the calculator is in degree mode, or the cosine of 30 radians if the calculator is in radian mode.
Given an angle in radians, use a graphing calculator to find the cosine.
Evaluate using a graphing calculator or computer.
Enter the following keystrokes:
Now that we can find the sine and cosine of an angle, we need to discuss their domains and ranges. What are the domains of the sine and cosine functions? That is, what are the smallest and largest numbers that can be inputs of the functions? Because angles smaller than and angles larger than can still be graphed on the unit circle and have real values of there is no lower or upper limit to the angles that can be inputs to the sine and cosine functions. The input to the sine and cosine functions is the rotation from the positive x -axis, and that may be any real number.
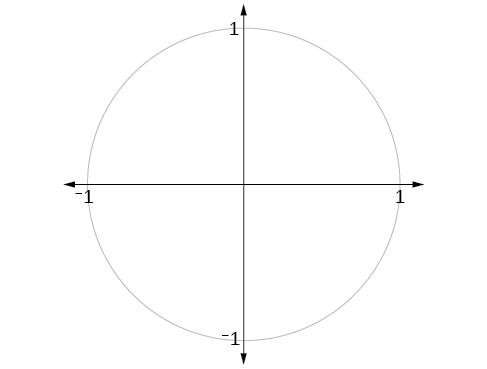
What are the ranges of the sine and cosine functions? What are the least and greatest possible values for their output? We can see the answers by examining the unit circle, as shown in [link] . The bounds of the x -coordinate are The bounds of the y -coordinate are also Therefore, the range of both the sine and cosine functions is
We have discussed finding the sine and cosine for angles in the first quadrant, but what if our angle is in another quadrant? For any given angle in the first quadrant, there is an angle in the second quadrant with the same sine value. Because the sine value is the y -coordinate on the unit circle, the other angle with the same sine will share the same y -value, but have the opposite x -value. Therefore, its cosine value will be the opposite of the first angle’s cosine value.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?