0.5 Lecture 6:continuous time fourier transform (ctft)  (Page 5/6)

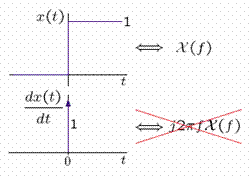
The derivative of x(t) is a unit impulse in time but the constant is lost. Thus, it must be included.

Hence,

$x\left(t\right)=u\left(t\right)=1/2+\left(1/2\right)\mathrm{sgn}\left(t\right)X\left(f\right)=\left(1/2\right)\delta \left(f\right)+\frac{1}{\mathrm{j2\pi f}}$

Two-minute miniquiz problem

Problem 17-1 — Step with a dc offset

Find the Fourier transform of x(t).

Solution

We can represent x(t) as

x(t) = 3/2 + (1/2)sgn(t).

Hence,

$X\left(f\right)=\left(3/2\right)\delta \left(f\right)+\frac{1}{\mathrm{j2\pi f}}$

9/ Causal cosinusoidal time function

A causal cosinusoid is a cosinusoid that starts at t = 0,

$x\left(t\right)=\cos \left(2{\mathrm{\pi f}}_{o}t\right)u\left(t\right)=\cos \left(2{\mathrm{\pi f}}_{o}t\right)\left(1/2+\left(1/2\right)\mathrm{sgn}\left(t\right)\right)$

Therefore,

$X\left(f\right)=F\left\{\cos \left(2{\mathrm{\pi f}}_{o}t\right)\right\}*F\left\{u\left(t\right)\right\}$ $=\left(1/2\right)\left(\delta \left(f-f_o\right)+\delta \left(f+f_o\right)\right)*\left(\left(1/2\right)\delta \left(f\right)+\frac{1}{\mathrm{j2\pi f}}\right)$ $=\left(1/4\right)\left(\delta \left(f-f_o\right)+\delta \left(f+f_o\right)\right)+\frac{1}{\mathrm{j4\pi }\left(f-f_o\right)}+\frac{1}{\mathrm{j4\pi }\left(f+f_o\right)}$ $=\left(1/4\right)\left(\delta \left(f-f_o\right)+\delta \left(f+f_o\right)\right)+\frac{f}{\mathrm{j2\pi }\left(f^2-{f_o}^2\right)}$

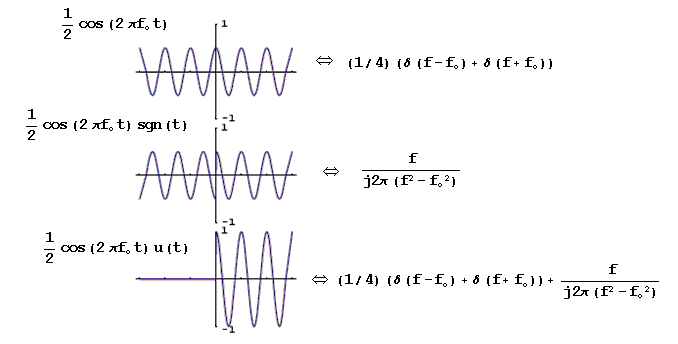
The Fourier and Laplace transforms of the causal cosinusoid are:

$\cos \left(2{\mathrm{\pi f}}_{o}t\right)u\left(t\right)\stackrel{F}{⟺}\left(1/4\right)\left(\delta \left(f-f_o\right)+\delta \left(f+f_o\right)\right)+\frac{f}{\mathrm{j2\pi }\left(f^2-{f_o}^2\right)}$ $\cos \left(2{\mathrm{\pi f}}_{o}t\right)u\left(t\right)\stackrel{F}{⟺}\frac{s}{s^2+{\left(2{\mathrm{\pi f}}_o\right)}^2}\mathrm{for}R\left\{s\right\}>0$

Therefore, just as with the unit step, the causal cosinusoid has poles on the jω axis, and the Fourier transform contains impulses at the frequencies of the poles.

A causal sinusoid is a sinusoid that starts at t = 0,

$x\left(t\right)=\sin \left(2{\mathrm{\pi f}}_{o}t\right)u\left(t\right)=\sin \left(2{\mathrm{\pi f}}_{o}t\right)\left(1/2+\left(1/2\right)\mathrm{sgn}\left(t\right)\right)$

Therefore,

$X\left(f\right)=F\left\{\sin \left(2{\mathrm{\pi f}}_{o}t\right)\right\}*F\left\{u\left(t\right)\right\}$ $=\left(1/2j\right)\left(\delta \left(f-f_o\right)-\delta \left(f+f_o\right)\right)*\left(\left(1/2\right)\delta \left(f\right)+\frac{1}{\mathrm{j2\pi f}}\right)$ $=\left(1/4\right)\left(\delta \left(f-f_o\right)-\delta \left(f+f_o\right)\right)+\frac{-1}{4\pi \left(f-f_o\right)}-\frac{-1}{4\pi \left(f+f_o\right)}$ $=\left(1/4j\right)\left(\delta \left(f-f_o\right)-\delta \left(f+f_o\right)\right)+\frac{-f_o}{2\pi \left(f^2-{f_o}^2\right)}$

10/ Rectangular pulse

a/ Rectangular pulse — derivation

The transform of the rectangular pulse x(t) is:

$X\left(f\right)={\int }_{-T/2}^{T/2}{\mathrm{Ae}}^{-\mathrm{j2\pi ft}}dt$ $=\frac{{\mathrm{Ae}}^{-\mathrm{j2\pi ft}}}{-\mathrm{j2\pi f}}{|}_{-T/2}^{T/2}$ $=\mathrm{AT}\frac{e^{\mathrm{j\pi fT}}-e^{-\mathrm{j\pi fT}}}{\mathrm{j2\pi fT}}$ $=\mathrm{AT}\left(\frac{\sin \mathrm{\pi fT}}{\mathrm{\pi fT}}\right)$

$\frac{\sin \mathrm{\pi fT}}{\mathrm{\pi fT}}={\{}_{0\mathrm{for}f=n/T,n\ne 0}^{1\mathrm{for}f=0}$

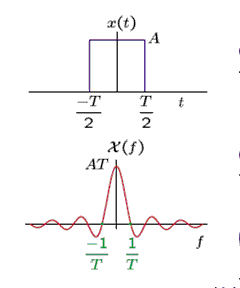
where n is an integer.

b/ Use of moment properties

From the moment properties we know that

$X\left(0\right)={\int }_{-\infty }^{\infty }x\left(t\right)\mathrm{dt}=\mathrm{AT}\mathrm{and}x\left(0\right)=A={\int }_{-\infty }^{\infty }X\left(f\right)\mathrm{df}$

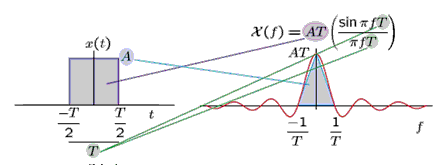
Note thatwhich is just the area of the inscribed triangle.

c/ Sinc function

The type of function arises so frequently that it is useful to

define the sinc function,

$\mathrm{sinc}\left(x\right)=\frac{\sin \mathrm{\pi x}}{\mathrm{\pi x}}$

Therefore,

$X\left(f\right)=\mathrm{AT}\left(\frac{\sin \mathrm{\pi fT}}{\mathrm{\pi fT}}\right)=\mathrm{ATsinc}\left(\mathrm{fT}\right)$

d/ Source of zeros in FT

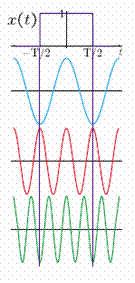
has zeros at f = n/T for n ≠ 0. What causes these zeros?

Note from the definition of the Fourier transform

$X\left(f\right)={\int }_{-\infty }^{\infty }x\left(t\right)e^{-\mathrm{j2\pi ft}}dt$ $={\int }_{-\infty }^{\infty }x\left(t\right)\left(\cos \left(2\mathrm{\pi ft}\right)-j\sin \left(2\mathrm{\pi ft}\right)\right)dt$

The duration of x(t) is T. Hence, the integral is zero for those frequencies whose periods are submultiples of T. These are the frequencies f = n/T where n ≠ 0. The examples show the frequencies f = 1/T , f = 2/T , and f = 3/T .

e/ Alternate derivation of FT

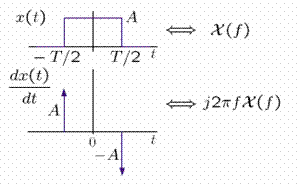
The Fourier transform can be found from

$\mathrm{j2\pi fX}\left(f\right)={\mathrm{Ae}}^{\mathrm{j2\pi f}\left(T/2\right)}-{\mathrm{Ae}}^{-\mathrm{j2\pi f}\left(T/2\right)}=2\mathrm{jA}\sin \left(\mathrm{\pi fT}\right)$ $X\left(f\right)=\mathrm{AT}\left(\frac{\sin \left(\mathrm{\pi fT}\right)}{\mathrm{\pi fT}}\right)$

f/ Effect of duration

Consider the sequence of rectangular pulses of the form

$x\left(t\right)={\{}_{0\mathrm{otherwise}}^{1/T\mathrm{for}t<\left|T/2\right|}\stackrel{F}{⟺}X\left(f\right)=\frac{\sin \left(\mathrm{\pi fT}\right)}{\mathrm{\pi fT}}$

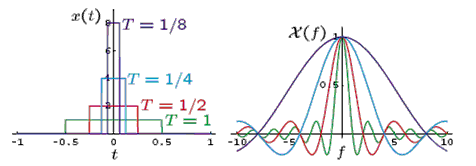
Note that as T decreases x(t) becomes tall and narrow and X(f) gets broader in frequency. Interpreted as generalized functions, x(t) → δ(t) and X(f) → 1.

11/ Triangular pulse

A triangular pulse is obtained by convolving a rectangular pulse with itself.

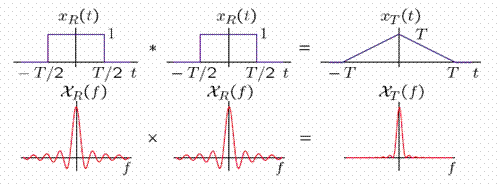
Since xT (t)=xR(t)*xR(t), the triangular pulse has the transform

$X_T\left(f\right)=X_R\left(f\right)\times X_R\left(f\right)={\left(T\frac{\sin \left(\mathrm{\pi fT}\right)}{\mathrm{\pi fT}}\right)}^2$

IV. FILTERING REVISITED