0.5 Lecture 6:continuous time fourier transform (ctft)  (Page 4/6)

$X\left(f\right)=\frac{1}{\mathrm{j2\pi f}+\alpha }$

$\left|X\left(f\right)\right|=\frac{1}{\sqrt{{\left(2\mathrm{\pi f}\right)}^2+{\alpha }^2}}\mathrm{and}\mathrm{\angle X}\left(f\right)=-{\tan }^{-1}\left(\frac{2\mathrm{\pi f}}{\alpha }\right)$

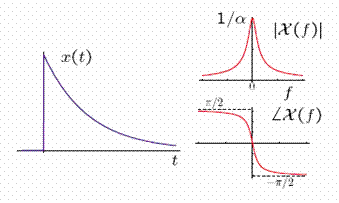
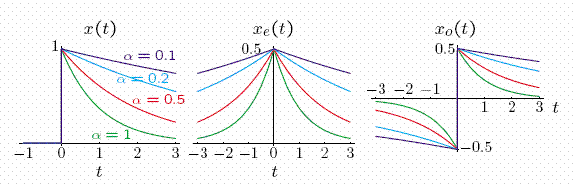
As α increases, the time function decays more rapidly and its duration (as measured by the time constant) decreases. As α increases, the Fourier transform width (as measured by its bandwidth) increases.

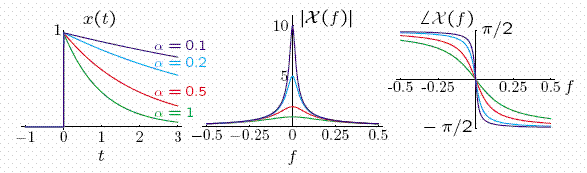
Thus, the width of the time function is inversely proportional to the width of the Fourier transform.

$X\left(f\right)=\frac{1}{\mathrm{j2\pi f}+\alpha }=\frac{\alpha }{{\left(2\mathrm{\pi f}\right)}^2+{\alpha }^2}+j\frac{-2\mathrm{\pi f}}{{\left(2\mathrm{\pi f}\right)}^2+{\alpha }^2}$

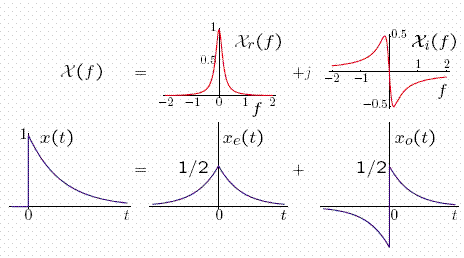
Therefore, we also have that

$x_e\left(t\right)=\left(1/2\right)e^{-\alpha \left|t\right|}\stackrel{F}{⟺}{X}_r\left(f\right)=\frac{\alpha }{{\left(2\mathrm{\pi f}\right)}^2+{\alpha }^2}$

$x_o\left(t\right)=\left(1/2\right)e^{-\alpha \left|t\right|}\mathrm{sgn}\left(t\right)\stackrel{F}{⟺}{\mathrm{jX}}_i\left(f\right)=j\frac{-2\mathrm{\pi f}}{{\left(2\mathrm{\pi f}\right)}^2+{\alpha }^2}$

Where

$\mathrm{sgn}\left(t\right)=\{\begin{array}{c}1\mathrm{for}t>0\\ -1\mathrm{for}t<0\end{array}$

Two-minute miniquiz problem

Problem 16-1 — Fourier transform of a unit step

The Laplace transform of a unit step is

$x\left(t\right)=u\left(t\right)\stackrel{F}{⟺}X\left(s\right)=\frac{1}{s}\mathrm{for}\sigma >0$

This suggests that the Fourier transform of the unit step is

$x\left(t\right)=u\left(t\right)\stackrel{F}{⟺}X\left(f\right)=\frac{1}{\mathrm{j2\pi f}}$

The Fourier transform of a causal exponential is

$x\left(t\right)=e^{-\mathrm{\alpha t}}u\left(t\right)\stackrel{F}{⟺}X\left(f\right)=\frac{1}{\mathrm{j2\pi f}+\alpha }$

This also suggests that the Fourier transform of the unit step is

$x\left(t\right)=u\left(t\right)\stackrel{F}{⟺}X\left(f\right)=\frac{1}{\mathrm{j2\pi f}}$

Explain why this cannot be the Fourier transform of a unit step.

Solution

$X\left(f\right)=\frac{1}{\mathrm{j2\pi f}}$

is an imaginary odd function of f. Hence, it must be the Fourier transform of an odd function of t. The unit step is neither an odd nor an even function of t.

The argument based on the Laplace transform of a step is fallacious because the Laplace transform of the step has a region of convergence that does not include the jω axis. Hence, we cannot simply substitute s = j2πf into the Laplace transform to obtain the Fourier transform. The second argument is fallacious because care has to be taken in evaluating.

$\frac{1}{\mathrm{j2\pi f}+\alpha }\mathrm{as}\alpha \to 0\mathrm{at}f=0$

7/ Unit step

To obtain the Fourier transform of the unit step we start with the Fourier transform of a causal exponential

$x\left(t\right)=e^{-\mathrm{\alpha t}}u\left(t\right)\stackrel{F}{⟺}X\left(f\right)=\frac{1}{\mathrm{j2\pi f}+\alpha }$

and examine the solution as α → 0.

Note that

$x\left(t\right)=e^{-\mathrm{\alpha t}}u\left(t\right)=x_e\left(t\right)+x_o\left(t\right)=\left(1/2\right)e^{-\alpha \left|t\right|}+\left(1/2\right)e^{-\alpha \left|t\right|}\mathrm{sgn}\left(t\right)$

Note that

$X\left(f\right)=\frac{1}{\mathrm{j2\pi f}+\alpha }=X_r\left(f\right)+{\mathrm{jX}}_i\left(f\right)=\frac{\alpha }{{\left(2\mathrm{\pi f}\right)}^2+{\alpha }^2}+j\frac{-2\mathrm{\pi f}}{{\left(2\mathrm{\pi f}\right)}^2+{\alpha }^2}$

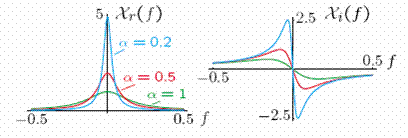
As α → 0, Xr(f) becomes tall and narrow and, as we shall see, its area is 1/2. Hence, as α → 0,

$X_r\left(f\right)\to \frac{1}{2}\delta \left(f\right)\mathrm{and}{\mathrm{jX}}_i\left(f\right)\to \frac{1}{\mathrm{j2\pi f}}$

We need to determine the area of Xr(f). Because

$x_e\left(t\right)\stackrel{F}{⟺}{X}_r\left(f\right)$ $x_e\left(0\right)={\int }_{-\infty }^{\infty }{X}_r\left(f\right)\mathrm{df}.$

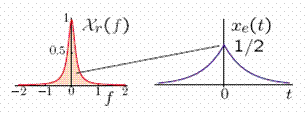
Hence,

$x_e\left(0\right)={\int }_{-\infty }^{\infty }{X}_r\left(f\right)\mathrm{df}=\frac{1}{2}$

Thus, we have

$u\left(t\right)=\frac{1}{2}+\frac{1}{2}\mathrm{sgn}\left(t\right)\stackrel{F}{⟺}F\left\{u\left(t\right)\right\}=\frac{1}{2}\delta \left(f\right)+\frac{1}{\mathrm{j2\pi f}}$

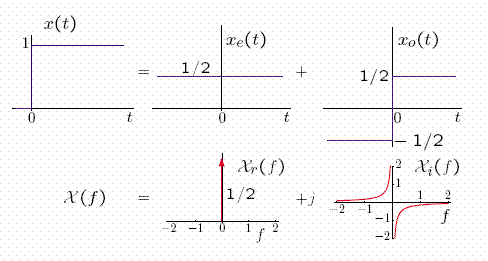
Unit step, bottom line

To summarize,

$u\left(t\right)\stackrel{F}{⟺}\frac{1}{s}\mathrm{for}R\left\{s\right\}>0$ $u\left(t\right)\stackrel{F}{⟺}\frac{1}{2}\delta \left(f\right)+\frac{1}{\mathrm{j2\pi f}}.$

Thus, if the Laplace transform is evaluated on the edge of the region of convergence, on the jω axis, then there is an impulse in the real part at the location of the pole.

8/ Signum and unit step function — another approach

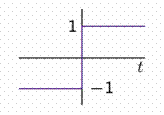
We illustrate a method for finding Fourier transforms using the Fourier transform properties and the Fourier transforms of simple time functions. Consider the time function x(t) = (1/2)sgn(t).

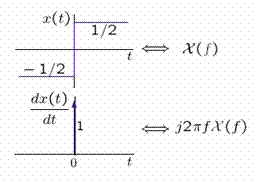
The derivative of x(t) is a unit impulse in time. Differentiation in time is equivalent to multiplying the transform by j2πf.

Hence,

$x\left(t\right)=\mathrm{sgn}\left(t\right)\stackrel{F}{⟺}X\left(f\right)=\frac{1}{\mathrm{j2\pi f}}$

The same approach can be used to find the Fourier transform of the step, x(t) = u(t), if some care is exercised. Note that u(t) = 1/2 + (1/2)sgn(t).