| << Chapter < Page | Chapter >> Page > |
Se tiene una forma de onda básica p(t) existente entre 0 y un valor D definido como la duración de dicha forma de onda, la misma se repite en el tiempo y se contamina con ruido en el canal de transmisión, la expresión para cada repetición de p(t) viene dada por:
La señal resultante se definirá como una sumatoria de ruido más expresiones semejantes a la ecuación 1 pero con diferentes valores de t 0 , adicionalmente algunas de las repeticiones podrían estar multiplicadas por alguna constante. Esta señal se puede filtrar con un sistema cuya respuesta impulsiva toma la siguiente forma:
Nótese que la variable t tiene signo negativo, esto se traduce en que dicha respuesta impulsiva está invertida con respecto al eje de las ordenadas.
Es necesario recordar que una forma de encontrar la señal de salida de un sistema en el dominio del tiempo es convolucionando la señal de entrada en el dominio del tiempo con la respuesta impulsiva del sistema. De esta forma se obtiene a la salida una señal con valores máximos situados en los puntos de ocurrencia de cada repetición.
Supóngase como señal de entrada la presente en la figura 1:
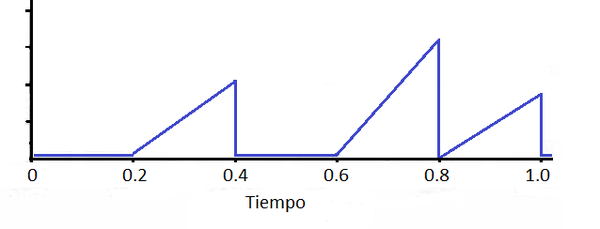
En vista de las formas de onda presentes, para las cuales el valor D es de 0.2, el filtro óptimo tendrá una respuesta impulsiva como la siguiente:
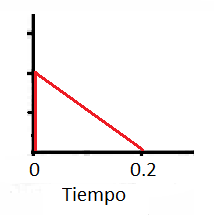
Al realizar la convolución entre la señal y el filtro, se obtendrá como resultado una señal parecida a la mostrada en verde en la figura 3:
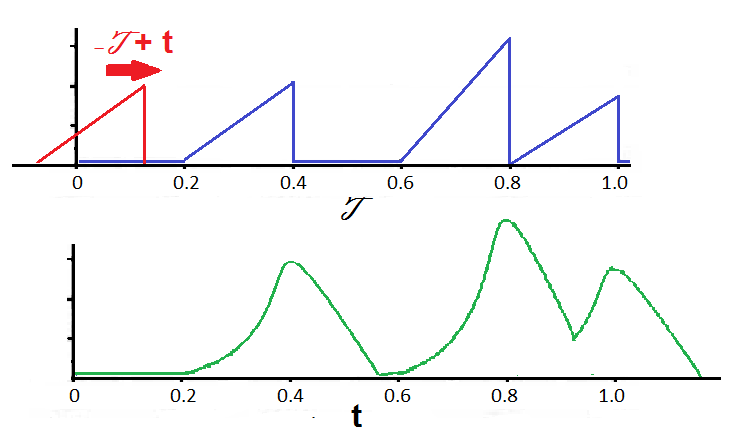
Esto se ha aplicado en diversas áreas, desde detección de señales digitales, ubicación de complejos QRS en un electrocardiograma, detección de capas geológicas para descubrir posibles yacimientos petroleros, etc.
¿Cómo debe ser la respuesta impulsiva del filtro óptimo para una señal digital binaria formada por pulsos rectangulares de duración Tbit?
La respuesta impulsiva será igual al pulso rectangular y tendrá una duración de Tbit, esto se debe a que si se invierte un pulso rectangular con respecto al eje vertical la forma de onda no cambiará (aplica para cualquier forma de onda horizontalmente simétrica).
¿Cómo varía la señal de salida si el filtro óptimo no toma su valor inicial en t=0?
Si el valor inicial del filtro óptimo se sitúa en t=0.3, por ejemplo, la única diferencia en la señal de salida será que la misma tendrá un desplazamiento hacia la izquierda de 0.3. Si esto ocurre en una aplicación de la vida real, es importante conocer el mencionado tiempo y tomar en cuenta el desplazamiento.
ESTE VINCULO contiene una carpeta con un programa realizado en MATLAB que aplica el Filtraje Óptimo a señales contaminadas con ruido. La carpeta incluye el .m y todos los archivos necesarios para su funcionamiento, si se elimina o renombra alguno de estos archivos, el programa podría no funcionar correctamente. La figura 4 contiene un video explicativo acerca del uso del programa.
Puede obtenerse también un programa realizado en LabVIEW acerca del mismo tema por medio de ESTE VINCULO . La carpeta incluye el .vi y todos los archivos necesarios para su funcionamiento. Igualmente, si se elimina o renombra alguno de estos archivos, el programa podría no funcionar correctamente. La figura 5 contiene un video explicativo acerca del uso del programa.

Notification Switch
Would you like to follow the 'Señales y sistemas en matlab y labview' conversation and receive update notifications?