| << Chapter < Page | Chapter >> Page > |
If we want to find the slope-intercept form without first writing the point-slope form, we could have recognized that the line crosses the y -axis when the output value is 7. Therefore, We now have the initial value and the slope so we can substitute and into the slope-intercept form of a line.
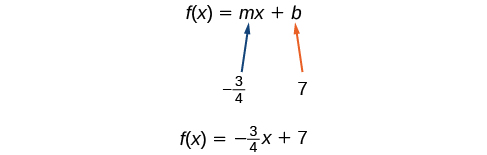
So the function is and the linear equation would be
Given the graph of a linear function, write an equation to represent the function.
Write an equation for a linear function given a graph of shown in [link] .
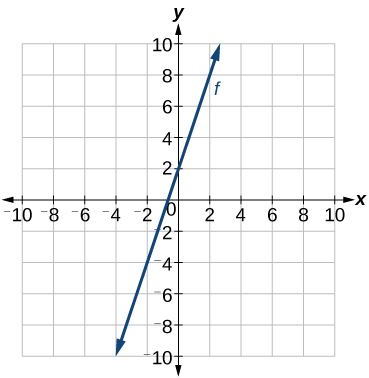
Identify two points on the line, such as and Use the points to calculate the slope.
Substitute the slope and the coordinates of one of the points into the point-slope form.
We can use algebra to rewrite the equation in the slope-intercept form.
Suppose Ben starts a company in which he incurs a fixed cost of $1,250 per month for the overhead, which includes his office rent. His production costs are $37.50 per item. Write a linear function where is the cost for items produced in a given month.
The fixed cost is present every month, $1,250. The costs that can vary include the cost to produce each item, which is $37.50. The variable cost, called the marginal cost, is represented by The cost Ben incurs is the sum of these two costs, represented by
If is a linear function, with and find an equation for the function in slope-intercept form.
We can write the given points using coordinates.
We can then use the points to calculate the slope.
Substitute the slope and the coordinates of one of the points into the point-slope form.
We can use algebra to rewrite the equation in the slope-intercept form.
If is a linear function, with and write an equation for the function in slope-intercept form.
In the real world, problems are not always explicitly stated in terms of a function or represented with a graph. Fortunately, we can analyze the problem by first representing it as a linear function and then interpreting the components of the function. As long as we know, or can figure out, the initial value and the rate of change of a linear function, we can solve many different kinds of real-world problems.
Given a linear function and the initial value and rate of change, evaluate

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?