| << Chapter < Page | Chapter >> Page > |
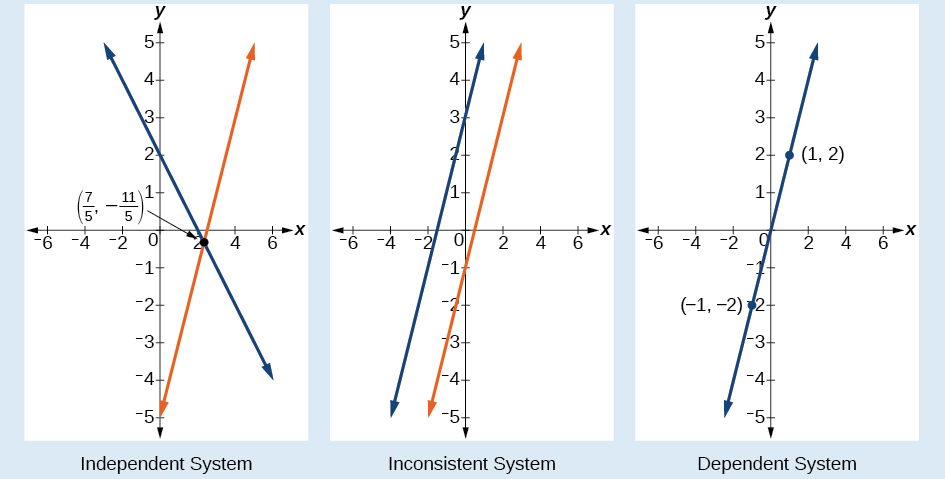
Another type of system of linear equations is an inconsistent system , which is one in which the equations represent two parallel lines. The lines have the same slope and different y- intercepts. There are no points common to both lines; hence, there is no solution to the system.
There are three types of systems of linear equations in two variables, and three types of solutions.
[link] compares graphical representations of each type of system.
Given a system of linear equations and an ordered pair, determine whether the ordered pair is a solution.
Determine whether the ordered pair is a solution to the given system of equations.
Substitute the ordered pair into both equations.
The ordered pair satisfies both equations, so it is the solution to the system.
Determine whether the ordered pair is a solution to the following system.
Not a solution.
There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.
Solve the following system of equations by graphing. Identify the type of system.
Solve the first equation for
Solve the second equation for
Graph both equations on the same set of axes as in [link] .
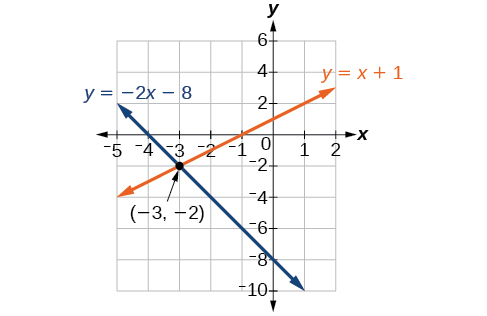
The lines appear to intersect at the point We can check to make sure that this is the solution to the system by substituting the ordered pair into both equations.
The solution to the system is the ordered pair so the system is independent.
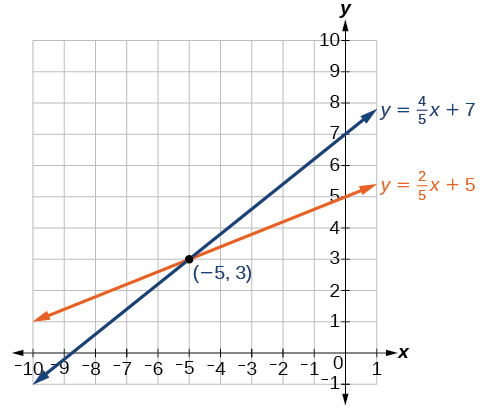
Solve the following system of equations by graphing.
The solution to the system is the ordered pair
Can graphing be used if the system is inconsistent or dependent?
Yes, in both cases we can still graph the system to determine the type of system and solution. If the two lines are parallel, the system has no solution and is inconsistent. If the two lines are identical, the system has infinite solutions and is a dependent system.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?