| << Chapter < Page | Chapter >> Page > |

John received an inheritance of $12,000 that he divided into three parts and invested in three ways: in a money-market fund paying 3% annual interest; in municipal bonds paying 4% annual interest; and in mutual funds paying 7% annual interest. John invested $4,000 more in municipal funds than in municipal bonds. He earned $670 in interest the first year. How much did John invest in each type of fund?
Understanding the correct approach to setting up problems such as this one makes finding a solution a matter of following a pattern. We will solve this and similar problems involving three equations and three variables in this section. Doing so uses similar techniques as those used to solve systems of two equations in two variables. However, finding solutions to systems of three equations requires a bit more organization and a touch of visual gymnastics.
In order to solve systems of equations in three variables, known as three-by-three systems, the primary tool we will be using is called Gaussian elimination , named after the prolific German mathematician Karl Friedrich Gauss . While there is no definitive order in which operations are to be performed, there are specific guidelines as to what type of moves can be made. We may number the equations to keep track of the steps we apply. The goal is to eliminate one variable at a time to achieve upper triangular form , the ideal form for a three-by-three system because it allows for straightforward back-substitution to find a solution which we call an ordered triple . A system in upper triangular form looks like the following:
The third equation can be solved for and then we back-substitute to find and To write the system in upper triangular form, we can perform the following operations:
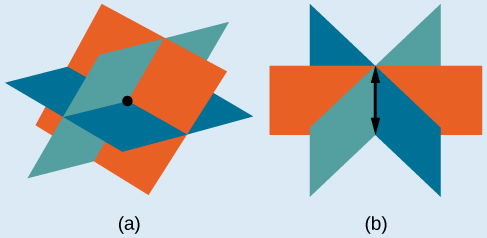
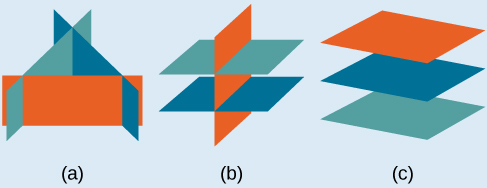
The solution set to a three-by-three system is an ordered triple Graphically, the ordered triple defines the point that is the intersection of three planes in space. You can visualize such an intersection by imagining any corner in a rectangular room. A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.
[link] and [link] illustrate possible solution scenarios for three-by-three systems.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?