| << Chapter < Page | Chapter >> Page > |
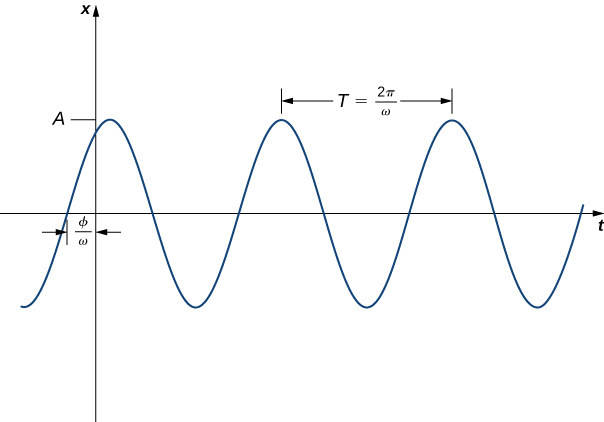
The function can be written in the form where and
Note that when using the formula to find we must take care to ensure is in the right quadrant ( [link] ).
Express the following functions in the form What is the frequency of motion? The amplitude?
Express the function in the form What is the frequency of motion? The amplitude?
With the model just described, the motion of the mass continues indefinitely. Clearly, this doesn’t happen in the real world. In the real world, there is almost always some friction in the system, which causes the oscillations to die off slowly—an effect called damping . So now let’s look at how to incorporate that damping force into our differential equation.
Physical spring-mass systems almost always have some damping as a result of friction, air resistance, or a physical damper, called a dashpot (a pneumatic cylinder; see [link] ).
Because damping is primarily a friction force, we assume it is proportional to the velocity of the mass and acts in the opposite direction. So the damping force is given by for some constant Again applying Newton’s second law, the differential equation becomes
Then the associated characteristic equation is
Applying the quadratic formula, we have
Just as in Second-Order Linear Equations we consider three cases, based on whether the characteristic equation has distinct real roots, a repeated real root, or complex conjugate roots.
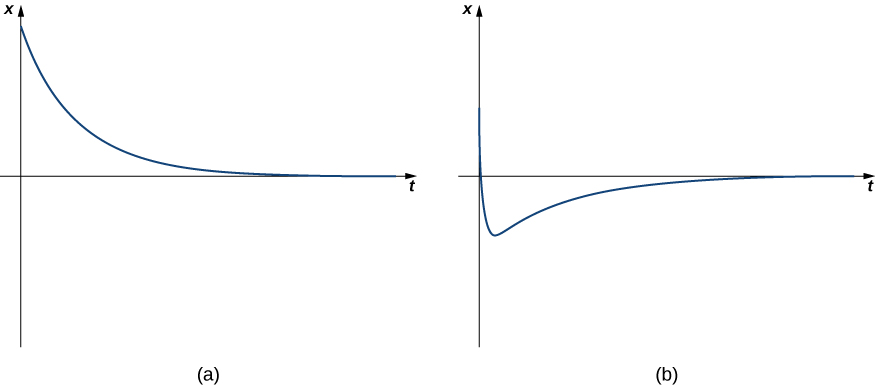
In this case, we say the system is overdamped . The general solution has the form
where both and are less than zero. Because the exponents are negative, the displacement decays to zero over time, usually quite quickly. Overdamped systems do not oscillate (no more than one change of direction), but simply move back toward the equilibrium position. [link] shows what typical critically damped behavior looks like.
A 16-lb mass is attached to a 10-ft spring. When the mass comes to rest in the equilibrium position, the spring measures 15 ft 4 in. The system is immersed in a medium that imparts a damping force equal to times the instantaneous velocity of the mass. Find the equation of motion if the mass is pushed upward from the equilibrium position with an initial upward velocity of 5 ft/sec. What is the position of the mass after 10 sec? Its velocity?
The mass stretches the spring 5 ft 4 in., or ft. Thus, so We also have so the differential equation is
Multiplying through by 2 gives which has the general solution
Applying the initial conditions, and we get
After 10 sec the mass is at position
so it is, effectively, at the equilibrium position. We have so after 10 sec the mass is moving at a velocity of
After only 10 sec, the mass is barely moving.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?