| << Chapter < Page | Chapter >> Page > |
That is ψ(z,t) = ψ 0 Exp[j(ωt-kz)]................. 1.85
An electron in 1-D potential box of width dimension L will follow the boundary conditions as given in the table and as shown in Figure 1.13(electron in a infinite potential well).
| k1 | k2 | k3 | k4 | |
| L | λ/2 | λ | 3λ/2 | 2λ |
| λ | 2L | L | 2L/3 | L/2 |
| k =2π/λ | 2π/(2L) | 2π/(L) | 2π/(2L/3) | 2π/(L/2) |
| k | 1×(π/L) | 2×(π/L) | 3×(π/L) | 4×(π/L) |
Therefore k n = n×(π/L)= wave vector of matter wave;
From Chapter1_part 3 and Chapter_part 6 we know that :
k z = √(2mE)/ћ=k; ..............1.86
Since the linear array has a period of L cm hence the matter wave has wave vector which is an integer multiple of (π/L) as shown in the Table above.
From Eq.(1.86) we obtain:
E = (ћ k z )^ 2 /(2m) = p z^ 2 /(2m) ..........1.87
Equation(1.87) gives us the energy distribution with respect to momentum vector (p z ) or wave vector (k z ) . This distribution is continuous and parabolic and is shown in Figure( 1.45). This is what would be expected for electron in free space. We get this result here because a very wide potential well with a flat bottom acts as a free and unbounded space for electron under consideration.

Figure. 1.45. Energy Distribution for electron in a very wide potential box.
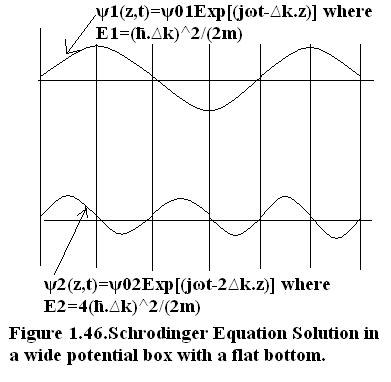
Figure 1.46. Schrodinger Equation Solution in a wide potential box with a flat bottom.
In Figure 1.46 the progressive wave solutions of the Schrodinger Equation is shown when applied to flat bottomed potential box. The solutions are:
First principal quantum number: ψ 1 (z,t)=ψ 01 Exp[(jωt-∆k.z)] where E 1 =(ћ.∆k) 2 /(2m);
Second principal quantum number: ψ 2 (z,t)=ψ 02 Exp[(jωt-2∆k.z)] where E 2 =4(ћ.∆k) 2 /(2m);
……………………………………………………………………………………………..
nth principal quantum number: ψ n (z,t)=ψ 0n Exp[(jωt-n∆k.z)] where E n =n 2 .(ћ.∆k) 2 /(2m);
Here ∆k = (π/L) is a very small quantity therefore E 1 , E 2 ,……. E n constitute a continuous spectrum of energy.
Since we have semi-infinite crystal of length L along z-axis hence each progressive wave has a periodicity of 2L, L, 2L/3, L/2, ……2L/n
Hence ψ n (z) = ψ n (z+2L/n)
When we replace a flat bottom by undulating bottom due to periodic potential variation due to lattice centres then we have a modulation effect on the progressive waves. As we had already mentioned in Fig(1.44) the periodicity of this potential variation is ‘a’ Å. Mathematical formulation of this modulation effect is difficult therefore we will give a graphical description of this modulation.
Periodic potential field is created by the lattice centers. Each lattice center is a potential well. If the potential well is of width W then electrons exist as standing waves of wavelengths (already shown in Figure 1.13)
2W, W, (2/3)W, W/2………
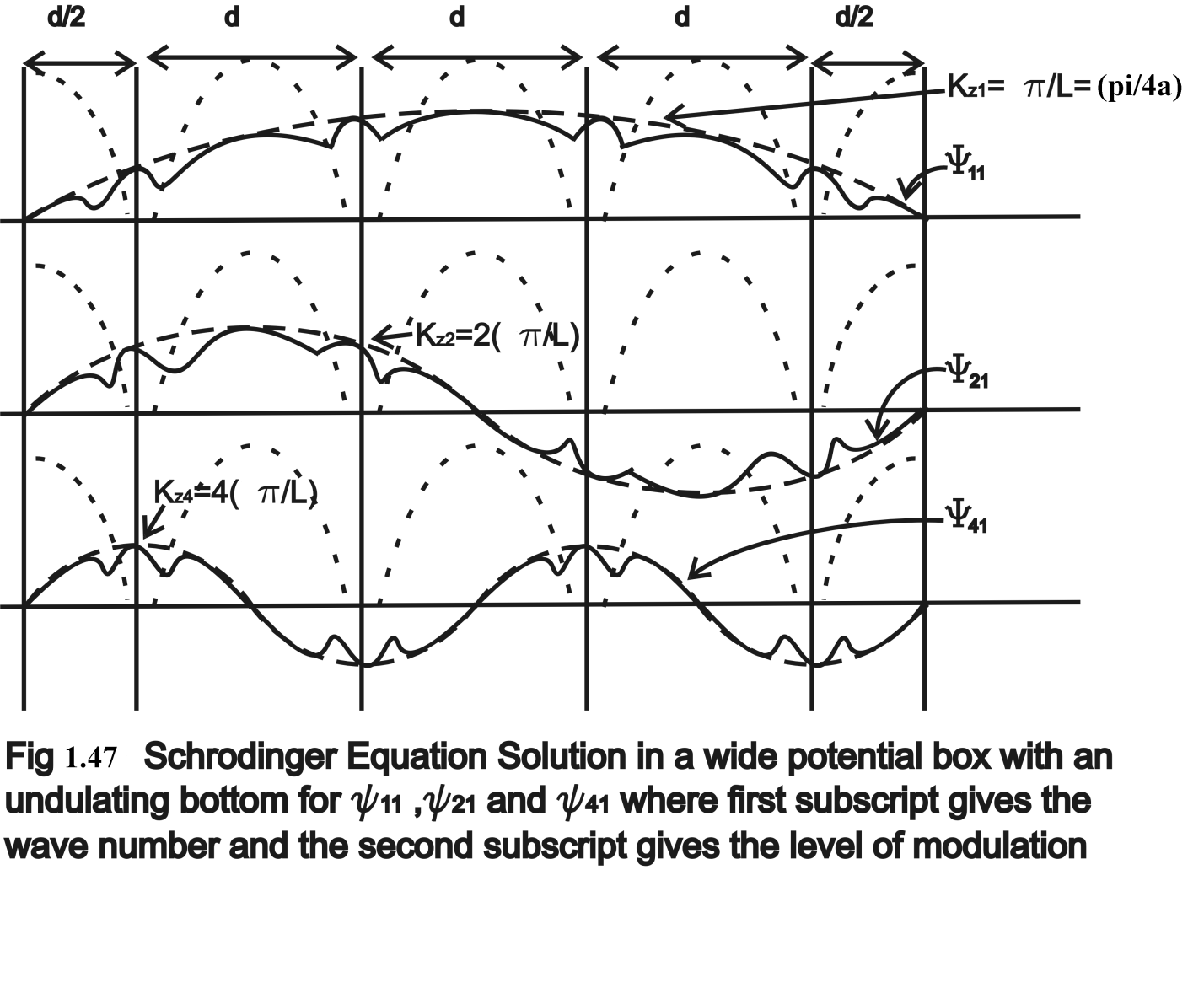
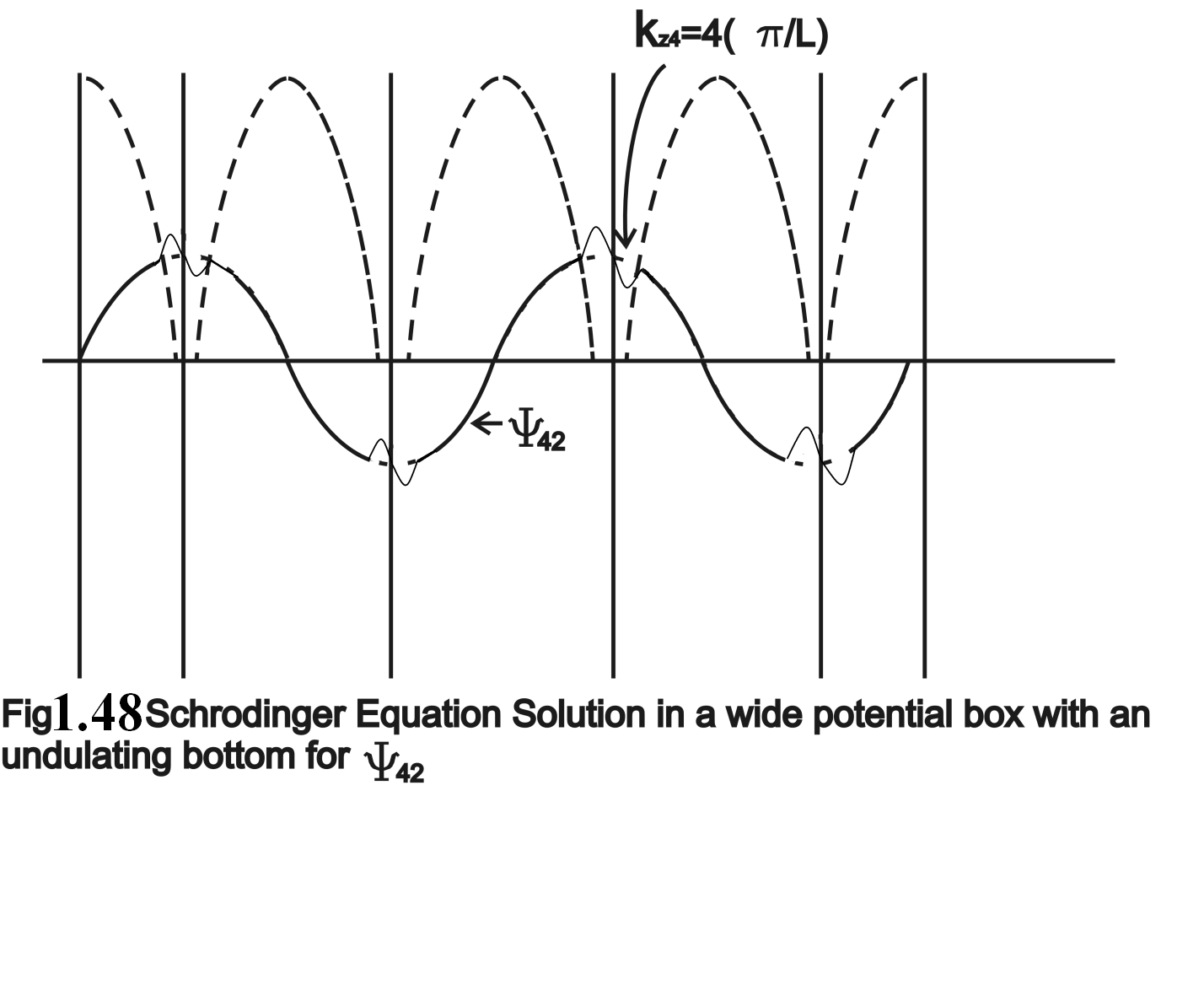
Figure 1.48. Schrodinger Equation Solution in a wide potential box with an undulating bottom for ψ 42
In Figure 1.47 and 1.48 we show the modulation effect of the lattice centers. The modulation is caused in the same way as the standing wave is created in the potential wells. Thus in Kronig-Penney Model solution ψ nj there are two quantum numbers:
n is the principle quantum number which decides the wave vector of the electron and which is a multiple of (π/L) hence the wave vector is k z = n.(π/L). This result has been explained in the preceding paragraph.

Notification Switch
Would you like to follow the 'Solid state physics and devices-the harbinger of third wave of civilization' conversation and receive update notifications?