| << Chapter < Page | Chapter >> Page > |
E= (1/2)m e v 2 – (q 2 )/( 4πε 0. r n ) 1.30
From Eq.(1.25), m e .v 2 = q 2 /(4πε 0. r n )
Substituting the above expression in Eq.(1.30)
E = - (1/2)m e v 2 1.31
In Betatron, the Lorentz [Appendix XXIX ] force provides the centripetal force to balance the centrifugal force created by the orbiting electron. Lorentz force is the motion created by left hand rule when a wire carrying current interacts with the transverse magnetic field. Lorentz force is given by Bqv where B is the transverse magnetic field and v is the linear velocity of the charge.
Therefore the equation of motion is:
Centripetal force = Bqv and centrifugal force = (mv 2 )/r
Therefore (1/r)m e v 2 = Bqv 1.32
In Betatron, the orbiting electron is unbounded and is orbiting at macroscopic level hence it can be analyzed by the classical theory. Here the orbital radius can assume a continuum of values hence when electron emits synchrotron radiation it traverses a collapsing spiral path towards the center. When the electron’s energy is boosted by an oscillating electric field then electron traverses an outward expanding spiral path. Both these conditions once of emission and the other of absorption is shown in Fig(1.15).
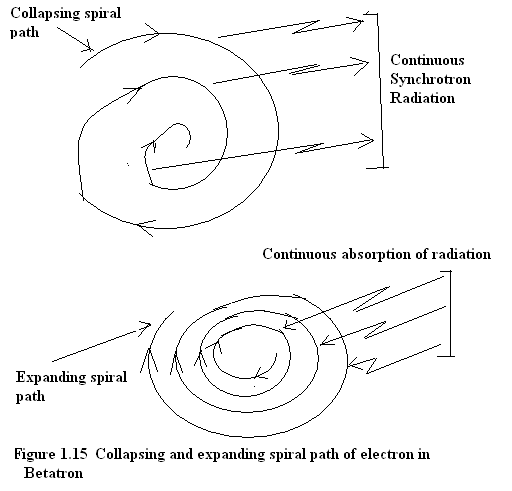
Figure 1.15 The inward collapsing spiral path of electron when emitting synchrotron radiation and the outward expanding spiral path of electron when boosted by alternating electric field.
This classical scenario is applicable to particles traversing circular paths at macroscopic scales. This is applicable to Betatron as well as to Synchrotron. But this picture completely fails at the Atomic scale.
For a Hydrogen Atom from Eq.(1.25) and (1.31) we obtain the following equation:
E = -q 2 /(8πε 0 r n )
Multiplying numerator and denominator by r n on RHS we get:
E = -[q 2 /(8πε 0 r n 2 )] ×r n
Substituting the value of r n from Eq.(1.26) we get:
E = -[q 2 /(8πε 0 r n 2 )]× (n 2 .h 2 .ε 0 /(m e .q 2 .π))
Simplifying the expression we get:
E = -(n 2 /(2m e .r n 2 ))(ћ 2 ) 1.33
For the bounded electron , the orbital radii are quantized hence total energy in the permissible orbits are also quantized. Substituting Eq.(1.26) in Eq.(1.33) we obtain:
E = -(1/(32π 2 )(m e q 4 / (ћ 2 ε 0 2 n 2 ))Joules 1.34
Putting Eq.(1.26) in Eq.(1.34) and rearranging the terms we get;
E×r n = - (q 2 /(8πε 0 ))
Substituting the value of
r n = n 2 ×(0.529Å) in the above Equation we get the following Eq. for Hydrogen Atom:
E = - (q 2 /(8πε 0 n 2 ×0.529Å))
Substituting the values:
E = -(13.6eV/n 2 ) 1.35
In Figure(1.16), the permissible energy states for an electron in a hydrogen potential well is illustrated.
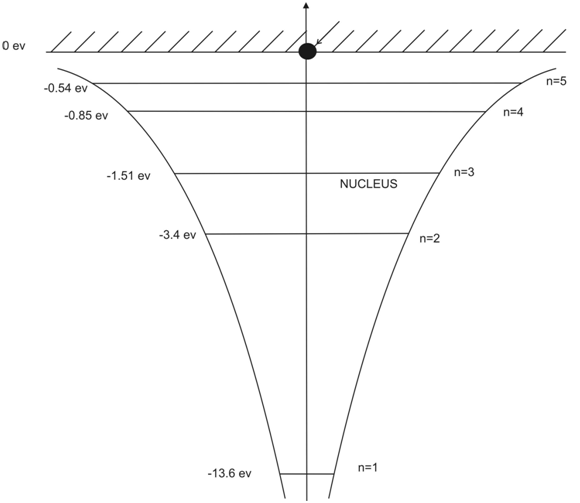
Figure 1.16. The quantized energy states of an electron in a hydrogen potential well.
Table(1.3) Discrete Energy States of Electron in Hydrogen Atom.
| n | E n |
| 1 | -13.6 eV |
| 2 | -3.4eV |
| 3 | -1.5eV |
| 4 | -0.85eV |
In Hydrogen atom the electron is 13.6eV below zero hence we say an electron having principal quantum number n=1 is in a potential well -13.6eV deep. Therefore Ionization Energy of Hydrogen is 13.6eV.
Two Hydrogen atoms when brought together form a very strong covalent bond by pairing the two outer electrons and completing the octave condition of the orbit corresponding to n=1.
What this means that n=1 orbit or K Shell can accommodate only two electrons to completely fill up the available states in K Shell. Each Atom completes the octave by sharing each other’s electron for 50% of the time and thereby achieve the Gibb’s free Energy Minima. This Minima ensures a stable configuration to the Hydrogen molecule. This energy minima is - 4.5eV. In other words the binding energy of the Hydrogen molecule is 4.5eV.
If Hydrogen gas is heated to T 1 = 15.6×10 4 Kelvin , the thermal energy imparted is kT 1 =13.4eV. Since this exceeds 4.5eV hence Hydrogen Molecule dissociates into two independent Hydrogen Atoms. And there is sufficient energy for the first ionization of Hydrogen Atom. When electron from K Shell is removed from the atom then we have First Ionization. If electron is removed from L Shell then we have Second Ionization and so on. We will see later that in the beginning when Big Bang took place the matter was in gluonic state and then in plasma state. Radiation was coupled with Matter. After 300,000 years when temperature fell to 4000K then plasma neutralized and radiation decoupled from matter and as Universe expanded this radiation went on cooling and today it appears as 3Kelvin relic radiation or as Cosmic Microwave Back Ground (CMB)Radiation and it carries the footprint of matter distribution as it was at the time of decoupling i.e. 300,000 years after the Big Bang. This CMB Radiation has hot spots meaning by there are clumping of matter in certain parts of space and these matter clumps acted as the nucleus of Galaxy Growth. CMB Radiation was isotropic then matter density would be homogeneous through out the Universe and there would have been no evolution of Galaxies, stars and planets.
At the Angstrom scale, only Quantum Mechanics correctly explains the behaviour of a bound electron in an Atomic potential well. This is confirmed by experimental observations. Experimentally it has been found that every element has its characteristic line spectrum. The line spectra could be of emissive type or absorption type.
When an excited element comes down to the ground state, it gives off certain characteristic wavelengths . This is called the emissive line spectra.
When a ground element intercepts an incident light, it absorbs certain characteristic wavelengths creating dark fringes in the spectrum of the resulting light. This is described as the absorption spectra of the given element.
During the period 1885-1908, the characteristic spectra was described by the following equation:
Ν = ν/c = 1/λ = R(1/n 2 2 - 1/n 1 2 ) 1.36
Where ν frequency of the transverse electro-magnetic wave;
Wavelength = λ;
Velocity of light = c;
Wave number = N;
Rydberg constant = 109677.6 cm -1 ;
n 1 = 1,2,3…..;
n 2 = 2,3,4,……;
The prominent Scientists associated with spectrum research at the time were Ritz, Rydberg and Barmer [Appendix XXX] .
Neil Bohr was able to give a theoretical explanation for Eq.(1.36) and theoretically derive Rydberg Constant.

Notification Switch
Would you like to follow the 'Solid state physics and devices-the harbinger of third wave of civilization' conversation and receive update notifications?