| << Chapter < Page | Chapter >> Page > |
A hardware store sells 16-ft ladders and 24-ft ladders. A window is located 12 feet above the ground. A ladder needs to be purchased that will reach the window from a point on the ground 5 feet from the building. To find out the length of ladder needed, we can draw a right triangle as shown in [link] , and use the Pythagorean Theorem.
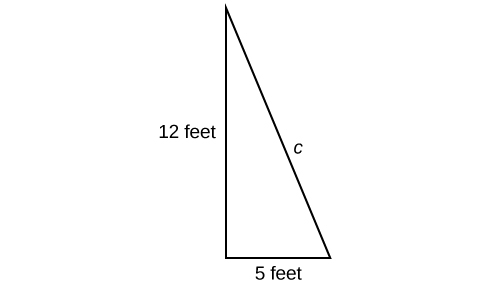
Now, we need to find out the length that, when squared, is 169, to determine which ladder to choose. In other words, we need to find a square root. In this section, we will investigate methods of finding solutions to problems such as this one.
When the square root of a number is squared, the result is the original number. Since the square root of is The square root function is the inverse of the squaring function just as subtraction is the inverse of addition. To undo squaring, we take the square root.
In general terms, if is a positive real number, then the square root of is a number that, when multiplied by itself, gives The square root could be positive or negative because multiplying two negative numbers gives a positive number. The principal square root is the nonnegative number that when multiplied by itself equals The square root obtained using a calculator is the principal square root.
The principal square root of is written as The symbol is called a radical , the term under the symbol is called the radicand , and the entire expression is called a radical expression .
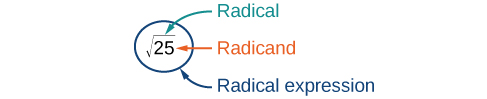
The principal square root of is the nonnegative number that, when multiplied by itself, equals It is written as a radical expression , with a symbol called a radical over the term called the radicand :
Does
No. Although both and are the radical symbol implies only a nonnegative root, the principal square root. The principal square root of 25 is
Evaluate each expression.
For can we find the square roots before adding?
No. This is not equivalent to The order of operations requires us to add the terms in the radicand before finding the square root.
To simplify a square root, we rewrite it such that there are no perfect squares in the radicand. There are several properties of square roots that allow us to simplify complicated radical expressions. The first rule we will look at is the product rule for simplifying square roots, which allows us to separate the square root of a product of two numbers into the product of two separate rational expressions. For instance, we can rewrite as We can also use the product rule to express the product of multiple radical expressions as a single radical expression.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?