| << Chapter < Page | Chapter >> Page > |
Find an angle that is coterminal with an angle measuring where
Given an angle with measure less than find a coterminal angle having a measure between and
Show the angle with measure on a circle and find a positive coterminal angle such that
Since is half of we can start at the positive horizontal axis and measure clockwise half of a angle.
Because we can find coterminal angles by adding or subtracting a full rotation of we can find a positive coterminal angle here by adding
We can then show the angle on a circle, as in [link] .
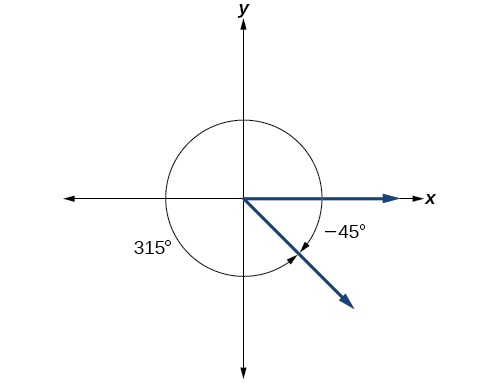
Find an angle that is coterminal with an angle measuring such that
We can find coterminal angles measured in radians in much the same way as we have found them using degrees. In both cases, we find coterminal angles by adding or subtracting one or more full rotations.
Given an angle greater than find a coterminal angle between 0 and
Find an angle that is coterminal with where
When working in degrees, we found coterminal angles by adding or subtracting 360 degrees, a full rotation. Likewise, in radians, we can find coterminal angles by adding or subtracting full rotations of radians:
The angle is coterminal, but not less than so we subtract another rotation.
The angle is coterminal with as shown in [link] .
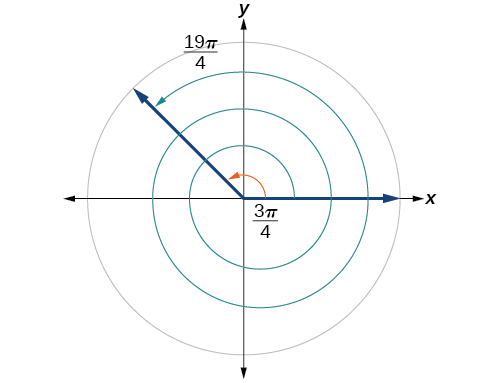
Find an angle of measure that is coterminal with an angle of measure where
Recall that the radian measure of an angle was defined as the ratio of the arc length of a circular arc to the radius of the circle, From this relationship, we can find arc length along a circle, given an angle.
In a circle of radius r , the length of an arc subtended by an angle with measure in radians, shown in [link] , is
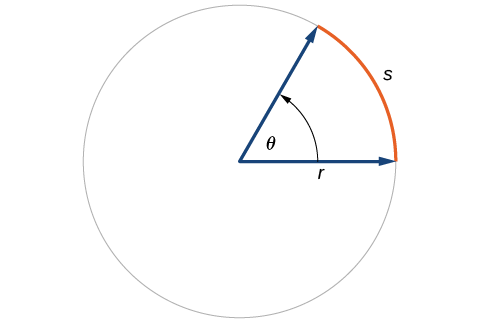
Given a circle of radius calculate the length of the arc subtended by a given angle of measure
Assume the orbit of Mercury around the sun is a perfect circle. Mercury is approximately 36 million miles from the sun.
Since Mercury completes 0.0114 of its total revolution in one Earth day, we can now find the distance traveled.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?