| << Chapter < Page | Chapter >> Page > |
We have learned how to solve systems of equations in two variables and three variables, and by multiple methods: substitution, addition, Gaussian elimination, using the inverse of a matrix, and graphing. Some of these methods are easier to apply than others and are more appropriate in certain situations. In this section, we will study two more strategies for solving systems of equations.
A determinant is a real number that can be very useful in mathematics because it has multiple applications, such as calculating area, volume, and other quantities. Here, we will use determinants to reveal whether a matrix is invertible by using the entries of a square matrix to determine whether there is a solution to the system of equations. Perhaps one of the more interesting applications, however, is their use in cryptography. Secure signals or messages are sometimes sent encoded in a matrix. The data can only be decrypted with an invertible matrix and the determinant. For our purposes, we focus on the determinant as an indication of the invertibility of the matrix. Calculating the determinant of a matrix involves following the specific patterns that are outlined in this section.
The determinant of a matrix, given
is defined as
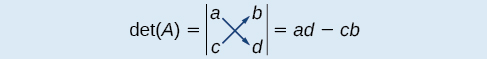
Notice the change in notation. There are several ways to indicate the determinant, including and replacing the brackets in a matrix with straight lines,
Find the determinant of the given matrix.
We will now introduce a final method for solving systems of equations that uses determinants. Known as
Cramer’s Rule , this technique dates back to the middle of the 18th century and is named for its innovator, the Swiss mathematician Gabriel Cramer (1704-1752), who introduced it in 1750 in
Cramer’s Rule will give us the unique solution to a system of equations, if it exists. However, if the system has no solution or an infinite number of solutions, this will be indicated by a determinant of zero. To find out if the system is inconsistent or dependent, another method, such as elimination, will have to be used.
To understand Cramer’s Rule, let’s look closely at how we solve systems of linear equations using basic row operations. Consider a system of two equations in two variables.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?