| << Chapter < Page | Chapter >> Page > |
An airplane is flying at an airspeed of 200 miles per hour headed on a SE bearing of 140°. A north wind (from north to south) is blowing at 16.2 miles per hour, as shown in [link] . What are the ground speed and actual bearing of the plane?

Ground speed refers to the speed of a plane relative to the ground. Airspeed refers to the speed a plane can travel relative to its surrounding air mass. These two quantities are not the same because of the effect of wind. In an earlier section, we used triangles to solve a similar problem involving the movement of boats. Later in this section, we will find the airplane’s groundspeed and bearing, while investigating another approach to problems of this type. First, however, let’s examine the basics of vectors.
A vector is a specific quantity drawn as a line segment with an arrowhead at one end. It has an initial point , where it begins, and a terminal point , where it ends. A vector is defined by its magnitude , or the length of the line, and its direction, indicated by an arrowhead at the terminal point. Thus, a vector is a directed line segment. There are various symbols that distinguish vectors from other quantities:
This last symbol has special significance. It is called the standard position . The position vector has an initial point and a terminal point To change any vector into the position vector, we think about the change in the x -coordinates and the change in the y -coordinates. Thus, if the initial point of a vector is and the terminal point is then the position vector is found by calculating
In [link] , we see the original vector and the position vector
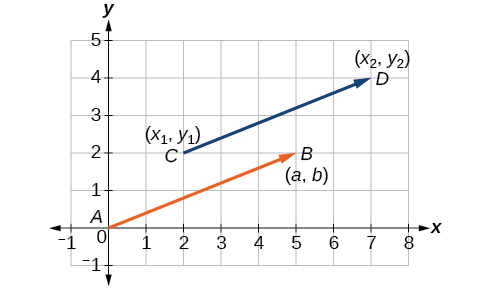
A vector is a directed line segment with an initial point and a terminal point. Vectors are identified by magnitude, or the length of the line, and direction, represented by the arrowhead pointing toward the terminal point. The position vector has an initial point at and is identified by its terminal point
Consider the vector whose initial point is and terminal point is Find the position vector.
The position vector is found by subtracting one x -coordinate from the other x -coordinate, and one y -coordinate from the other y -coordinate. Thus
The position vector begins at and terminates at The graphs of both vectors are shown in [link] .
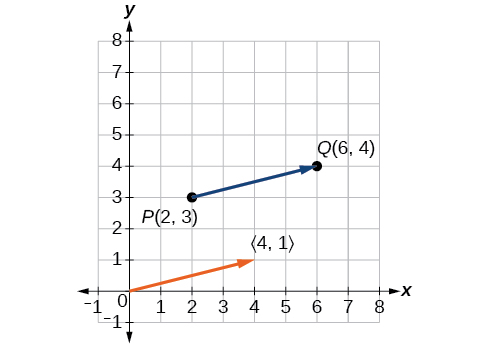
We see that the position vector is

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?