| << Chapter < Page | Chapter >> Page > |
For the equation what constants affect the range of the function and how do they affect the range?
The absolute value of the constant (amplitude) increases the total range and the constant (vertical shift) shifts the graph vertically.
How does the range of a translated sine function relate to the equation
How can the unit circle be used to construct the graph of
At the point where the terminal side of intersects the unit circle, you can determine that the equals the y -coordinate of the point.
For the following exercises, graph two full periods of each function and state the amplitude, period, and midline. State the maximum and minimum y -values and their corresponding x -values on one period for Round answers to two decimal places if necessary.
![A graph of (2/3)cos(x). Graph has amplitude of 2/3, period of 2pi, and range of [-2/3, 2/3].](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_202.jpg)
amplitude: period: midline: maximum: occurs at minimum: occurs at for one period, the graph starts at 0 and ends at
![A graph of 4sin(x). Graph has amplitude of 4, period of 2pi, and range of [-4, 4].](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_204.jpg)
amplitude: 4; period: midline: maximum occurs at minimum: occurs at one full period occurs from to
![A graph of cos(2x). Graph has amplitude of 1, period of pi, and range of [-1,1].](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_206.jpg)
amplitude: 1; period: midline: maximum: occurs at minimum: occurs at one full period is graphed from to
![A graph of 4cos(pi*x). Grpah has amplitude of 4, period of 2, and range of [-4, 4].](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_208.jpg)
amplitude: 4; period: 2; midline: maximum: occurs at minimum: occurs at
![A graph of 3sin(8(x+4))+5. Graph has amplitude of 3, range of [2, 8], and period of pi/4.](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_210.jpg)
amplitude: 3; period: midline: maximum: occurs at minimum: occurs at horizontal shift: vertical translation 5; one period occurs from to
![A graph of 5sin(5x+20)-2. Graph has an amplitude of 5, period of 2pi/5, and range of [-7,3].](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_212.jpg)
amplitude: 5; period: midline: maximum: occurs at minimum: occurs at phase shift: vertical translation: one full period can be graphed on to
For the following exercises, graph one full period of each function, starting at For each function, state the amplitude, period, and midline. State the maximum and minimum y -values and their corresponding x -values on one period for State the phase shift and vertical translation, if applicable. Round answers to two decimal places if necessary.
![A graph of -cos(t+pi/3)+1. Graph has amplitude of 1, period of 2pi, and range of [0,2]. Phase shifted pi/3 to the left.](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_214.jpg)
amplitude: 1 ; period: midline: maximum: occurs at maximum: occurs at minimum: occurs at phase shift: vertical translation: 1; one full period is from to
![A graph of -sin((1/2)*t + 5pi/3). Graph has amplitude of 1, range of [-1,1], period of 4pi, and a phase shift of -10pi/3.](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_216.jpg)
amplitude: 1; period: midline: maximum: occurs at minimum: occurs at phase shift: vertical shift: 0
Determine the amplitude, midline, period, and an equation involving the sine function for the graph shown in [link] .
![A sinusoidal graph with amplitude of 2, range of [-5, -1], period of 4, and midline at y=-3.](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_218.jpg)
amplitude: 2; midline: period: 4; equation:
Determine the amplitude, period, midline, and an equation involving cosine for the graph shown in [link] .
![A graph with a cosine parent function, with amplitude of 3, period of pi, midline at y=-1, and range of [-4,2]](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_219.jpg)
Determine the amplitude, period, midline, and an equation involving cosine for the graph shown in [link] .
![A graph with a cosine parent function with an amplitude of 2, period of 5, midline at y=3, and a range of [1,5].](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_220.jpg)
amplitude: 2; period: 5; midline: equation:
Determine the amplitude, period, midline, and an equation involving sine for the graph shown in [link] .
![A sinusoidal graph with amplitude of 4, period of 10, midline at y=0, and range [-4,4].](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_221.jpg)
Determine the amplitude, period, midline, and an equation involving cosine for the graph shown in [link] .
![A graph with cosine parent function, range of function is [-4,4], amplitude of 4, period of 2.](/ocw/mirror/col11667/m49387/CNX_Precalc_Figure_06_01_222.jpg)
amplitude: 4; period: 2; midline: equation:
Determine the amplitude, period, midline, and an equation involving sine for the graph shown in [link] .
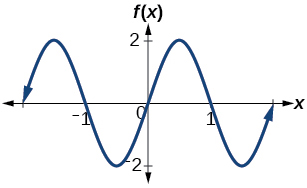
Determine the amplitude, period, midline, and an equation involving cosine for the graph shown in [link] .
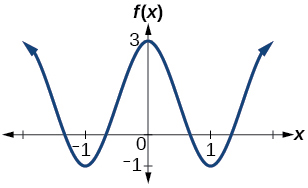
amplitude: 2; period: 2; midline equation:
Determine the amplitude, period, midline, and an equation involving sine for the graph shown in [link] .
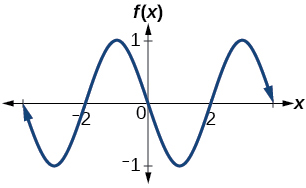
For the following exercises, let
On the maximum value(s) of the function occur(s) at what x -value(s)?
On the minimum value(s) of the function occur(s) at what x -value(s)?
Show that This means that is an odd function and possesses symmetry with respect to ________________.
For the following exercises, let
On find the x -values at which the function has a maximum or minimum value.
Graph on Explain why the graph appears as it does.
Graph on Did the graph appear as predicted in the previous exercise?
The graph appears linear. The linear functions dominate the shape of the graph for large values of
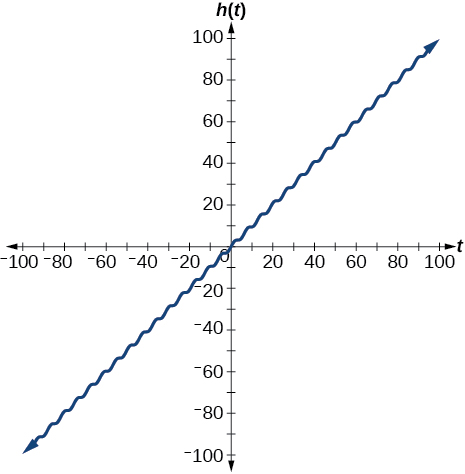
Graph on and verbalize how the graph varies from the graph of
Graph on the window and explain what the graph shows.
The graph is symmetric with respect to the y -axis and there is no amplitude because the function is not periodic.
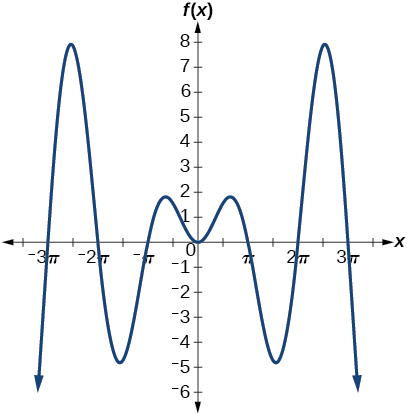
Graph on the window and explain what the graph shows.
A Ferris wheel is 25 meters in diameter and boarded from a platform that is 1 meter above the ground. The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 10 minutes. The function gives a person’s height in meters above the ground t minutes after the wheel begins to turn.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?