| << Chapter < Page | Chapter >> Page > |

Curved antennas, such as the ones shown in [link] , are commonly used to focus microwaves and radio waves to transmit television and telephone signals, as well as satellite and spacecraft communication. The cross-section of the antenna is in the shape of a parabola, which can be described by a quadratic function.
In this section, we will investigate quadratic functions, which frequently model problems involving area and projectile motion. Working with quadratic functions can be less complex than working with higher degree functions, so they provide a good opportunity for a detailed study of function behavior.
The graph of a quadratic function is a U-shaped curve called a parabola . One important feature of the graph is that it has an extreme point, called the vertex . If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value . In either case, the vertex is a turning point on the graph. The graph is also symmetric with a vertical line drawn through the vertex, called the axis of symmetry . These features are illustrated in [link] .
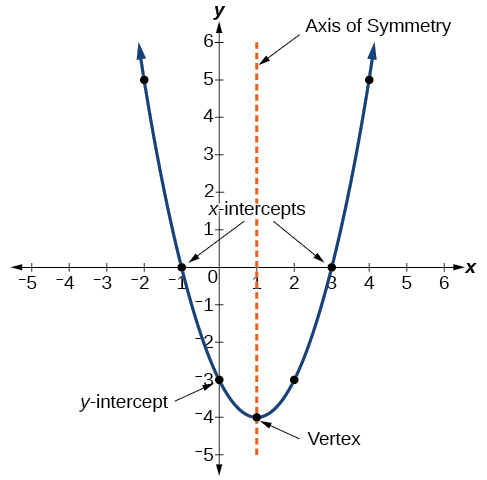
The y -intercept is the point at which the parabola crosses the y -axis. The x -intercepts are the points at which the parabola crosses the x -axis. If they exist, the x -intercepts represent the zeros , or roots , of the quadratic function, the values of at which
Determine the vertex, axis of symmetry, zeros, and intercept of the parabola shown in [link] .
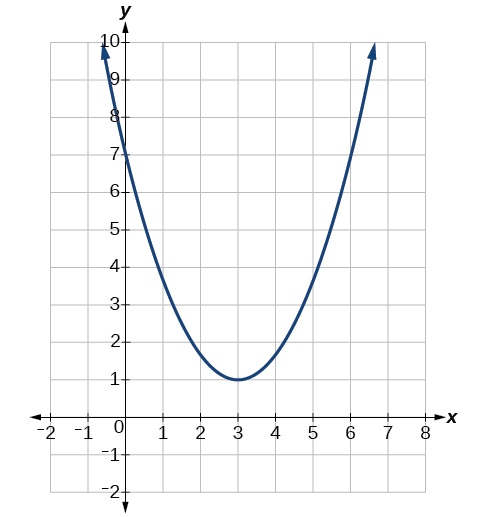
The vertex is the turning point of the graph. We can see that the vertex is at Because this parabola opens upward, the axis of symmetry is the vertical line that intersects the parabola at the vertex. So the axis of symmetry is This parabola does not cross the axis, so it has no zeros. It crosses the axis at so this is the y -intercept.
The general form of a quadratic function presents the function in the form
where and are real numbers and If the parabola opens upward. If the parabola opens downward. We can use the general form of a parabola to find the equation for the axis of symmetry.
The axis of symmetry is defined by If we use the quadratic formula, to solve for the intercepts, or zeros, we find the value of halfway between them is always the equation for the axis of symmetry.
[link] represents the graph of the quadratic function written in general form as In this form, and Because the parabola opens upward. The axis of symmetry is This also makes sense because we can see from the graph that the vertical line divides the graph in half. The vertex always occurs along the axis of symmetry. For a parabola that opens upward, the vertex occurs at the lowest point on the graph, in this instance, The intercepts, those points where the parabola crosses the axis, occur at and

Notification Switch
Would you like to follow the 'Selected topics in algebra' conversation and receive update notifications?