| << Chapter < Page | Chapter >> Page > |
In the following exercises, find the volume of the solid whose boundaries are given in rectangular coordinates.
is above the -plane, inside the cylinder and below the plane
is below the plane and inside the paraboloid
is located above the -plane, below outside the one-sheeted hyperboloid and inside the cylinder
is located inside the cylinder and between the circular paraboloids and
is located inside the sphere above the -plane, and inside the circular cone
is located outside the circular cone and between the planes and
is located outside the circular cone above the -plane, below the circular paraboloid, and between the planes
[T] Use a computer algebra system (CAS) to graph the solid whose volume is given by the iterated integral in cylindrical coordinates Find the volume of the solid. Round your answer to four decimal places.
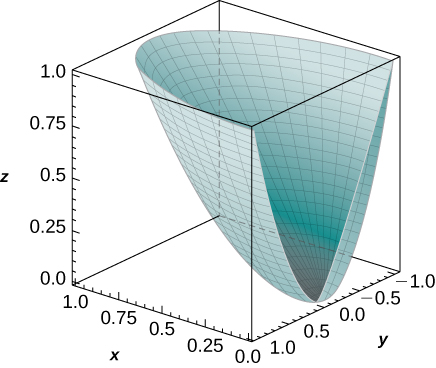
[T] Use a CAS to graph the solid whose volume is given by the iterated integral in cylindrical coordinates Find the volume of the solid Round your answer to four decimal places.
Convert the integral into an integral in cylindrical coordinates.
Convert the integral into an integral in cylindrical coordinates.
In the following exercises, evaluate the triple integral over the solid
is bounded above by the half-sphere with and below by the cone
is bounded above by the half-sphere with and below by the cone
Show that if is a continuous function on the spherical box then

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?