| << Chapter < Page | Chapter >> Page > |
APPENDIX XXXV _Schrodinger Equation and its solution.
To fully understand Schrodinger Equation we must understand the concept of operator associated with any physical observable (dynamical variable) and its canonical conjugate.
Translational momentum p is associated with the spatial coordinates: x, y and z;
Rotational momentum J is associated with the curvilinear coordinate θ;
Energy E is associated with temporal element time t.
We give the following excerpt from “ Basic Quantum Mechanics” Robert L. White, Publisher McGraw Hill, 1966.
The postulates of Quantum Mechanics:
POSTULATE 1. With every physical observable ‘a’, we may associate a mathematical operator A from whose properties we may deduce the possible results of measurements of the physical observable ‘a’. Measurement of a physical observable is analogous to taking a measurement. The result of measurement is ‘a n ’.
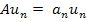
u n is a solution of the above equation. The above equation has a set of solutions which meet certain boundary conditions. This set of solutions are known as Eigen Functions.
In the above equation, operator A operates on the eigen function ‘u n ’ and generates an eigen value ‘a n ’ . If the eigen functions exist for discrete values of ‘a n ’ then we say we have DISCRETE eigenvalue spectrum.
If the eigen functions exist for continuous values of ‘a n ’ then we say we have CONTINUOUS eigenvalue spectrum.
POSTULATE 2. The only possible result of a measurement of the physical observable ‘a’ is one of the eigen values of operator A.
POSTULATE 3. For every dynamical system there exists a state function ψ which contains all the information that is known about the system. Ψ is the probability amplitude and |ψ| 2 is the probability density of obtaining a measurement ‘a n ’ while carrying out a series of measurements on observable ‘a’.
POSTULATE 4. If we know ψ for any system at any particular time , then the evolution of ψ at all subsequent times is determined by:
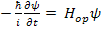
Where H op is the operator associated with the Hamiltonian of the system. Postulate 4 directly leads to Schrodinger Equation.
Operators of Quantum Mechanics are generally not commutative.
Commutator Bracket is [A,B] = (AB-BA) = -[B,A]
[A,A] = 0
[A,K] = 0 where K is a constant.
[A+B,C] = [A,C]+ [B,C]
[A,(BC)] = [A,B]C + B[A,C];
What the above properties imply is the following:
[Q j , Q k ] = 0;
Schrodinger in his classic formulation proposed a set of operators for quantum mechanical dynamical variables and their canonical conjugates.
| Dynamical Variable | Associated Operator |
| x → | x (multiply by x) |
| p x → |
|
| y → | y (multiply by y) |
| p y → |
|
| z → | z (multiply by z) |
| p z → |
|
| p → |
|
|
|
|
| t → |
|
We will consider the Hamiltonian Operator for conservative system:
H = T + qV where T is the Kinetic Energy and qV is the potential energy.
In translational motion:
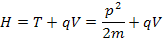
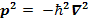
Therefore
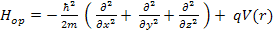
We let this Operator operate on a probability amplitude function ψ(r,t).
Therefore:
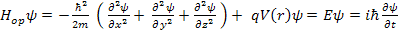
Eq XXXV.2 is defined as Schrodinger Equation.
Just as we used the separation of variables in solving the Wave Equation in Appendix XXXIV we will use separation of variables in this equation also. In addition we will consider this as 1-D problem with V(x) = 0.
Hence Schrodinger Equation reduces to:
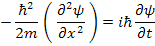
Let ψ(x,t) = ψ1(x).ψ2(t)
We assume ψ2(t) = Exp(-iωt) hence
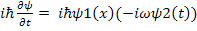
Therefore Right hand side of the Schrodinger equation is :
RHS = +ℏω
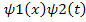
Therefore Schrodinger Equation reduces to:
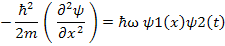
This simplifies to:
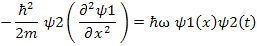
Ψ2(t) cancels out from both sides hence we have an ordinary linear differential equation namely:
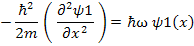
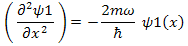
This is a second order ordinary differential equation with two roots namely ±i√(
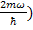
√(
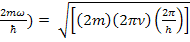
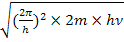
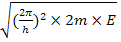
But E =
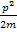
Therefore
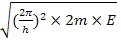
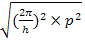
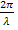
Hence ±√(
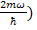
Therefore the solution is
Ψ(x,t) = ψ1(x)ψ2(t)
And ψ1(x) = AExp(+ik*x) + Bexp(-ik*x)
Therefore total solution is : Ψ(x,t) = ψ1(x)ψ2(t)
Or Ψ(x,t) = [AExp(+ik*x)+ Bexp(-ik*x)]Exp(-iωt)
Or Ψ(x,t) = AExp[-i(ωt-k*x)] + Bexp[-i(ωt+k*x)]→ These are two travelling waves: 1 st is moving forward and second is moving backward.
If V(x) = V 1 = constant then the Schrodinger equation will be :
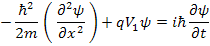
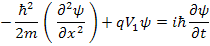
Again we apply the separation of variables method:
Let ψ(x,t) = ψ1(x).ψ2(t)
We assume ψ2(t) = Exp(-iωt) hence
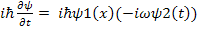
Therefore Right hand side of the Schrodinger equation is :
RHS = +ℏω
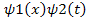
Therefore:
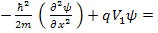
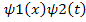
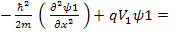
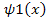
Rearranging the terms:
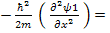
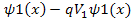
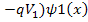
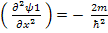
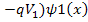
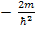
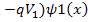
This also has two roots : ±i
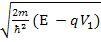
Therefore the solution is: Ψ(x,t) = AExp[-i(ωt-k**x)] + Bexp[-i(ωt+k**x)]
If E>qV 1 , we have imaginay roots of the ordinary linear differential equation and we get traveling waves as the solution.
But if E<qV 1 , we have real roots of the ordinary linear differential equation and we get exponentially decaying or exponentially growing solutions.

Notification Switch
Would you like to follow the 'Solid state physics and devices-the harbinger of third wave of civilization' conversation and receive update notifications?