2.4 Complex form of the fourier series

Signals, systems, and society Page 1 / 1

The trigonometric form of the Fourier Series, shown in [link] can be converted into a more convenient form by doing the following substitutions:

cos (n Ω_{0} t) = \frac{e^{j n Ω_{0} t} + e^{- j n Ω_{0} t}}{2}

sin (n Ω_{0} t) = \frac{e^{j n Ω_{0} t} - e^{- j n Ω_{0} t}}{j 2}

After some straight-forward rearranging, we obtain

x (t) = a_{0} + \sum_{n = 1}^{\infty} [\frac{a_{n} - j b_{n}}{2}] e^{j n Ω_{0} t} + \sum_{n = 1}^{\infty} [\frac{a_{n} + j b_{n}}{2}] e^{- j n Ω_{0} t}

Keeping in mind that $a_{n}$ and $b_{n}$ are only defined for positive values of $n$ , lets sum over the negative integers in the second summation:

x (t) = a_{0} + \sum_{n = 1}^{\infty} [\frac{a_{n} - j b_{n}}{2}] e^{j n Ω_{0} t} + \sum_{n = - 1}^{- \infty} [\frac{a_{- n} + j b_{- n}}{2}] e^{j n Ω_{0} t}

Next, let's assume that $a_{n}$ and $b_{n}$ are defined for both positive and negative $n$ . In this case, we find that $a_{n} = a_{- n}$ and $b_{n} = - b_{- n}$ , since

\begin{matrix} a_{- n} & = & \frac{2}{T} \int_{t_{0}}^{t_{0} + T} x (t) cos (- n Ω_{0} t) d t \\ = & \frac{2}{T} \int_{t_{0}}^{t_{0} + T} x (t) cos (n Ω_{0} t) d t \\ = & a_{n} \end{matrix}

and

\begin{matrix} b_{- n} & = & \frac{2}{T} \int_{t_{0}}^{t_{0} + T} x (t) sin (- n Ω_{0} t) d t \\ = & - \frac{2}{T} \int_{t_{0}}^{t_{0} + T} x (t) sin (n Ω_{0} t) d t \\ = & - b_{n} \end{matrix}

Using this fact, we can rewrite [link] as

x (t) = a_{0} + \sum_{n = 1}^{\infty} [\frac{a_{n} - j b_{n}}{2}] e^{j n Ω_{0} t} + \sum_{n = - 1}^{- \infty} [\frac{a_{n} - j b_{n}}{2}] e^{j n Ω_{0} t}

If we define The notation “ $\equiv$ " is often used instead of the “ $=$ " sign when defining a new variable. $c_{0} \equiv a_{0}$ , and

c_{n} \equiv \frac{a_{n} - j b_{n}}{2}

then we can rewrite [link] as

x (t) = \sum_{n = - \infty}^{\infty} c_{n} e^{j n Ω_{0} t}

which is called the complex form of the Fourier Series. Note that since $a_{- n} = a_{n}$ and $b_{- n} = - b_{n}$ , we have

c_{- n} = c_{n}^{*}

This means that

|c_{- n}| = |c_{n}|

and

∠ c_{- n} = - ∠ c_{n}

Next, we must find formulas for finding the $c_{n}$ given $x (t)$ . We first look at a property of complex exponentials:

\int_{t_{0}}^{t_{0} + T} e^{j k Ω_{0} t} d t = \{\begin{matrix} T, & k = 0 \\ 0, & otherwise \end{matrix})

To see this, we note that

\int_{t_{0}}^{t_{0} + T} e^{j k Ω_{0} k t} d t = \int_{t_{0}}^{t_{0} + T} cos (k Ω_{0} t) + j \int_{t_{0}}^{t_{0} + T} sin (k Ω_{0} t) d t

It's easy to see that $k Ω_{0}$ also has period $T$ , hence the integral is over $k$ periods of $cos (k Ω_{0} t)$ and $sin (k Ω_{0} t)$ . Therefore, if $k \neq 0$ , then

\int_{t_{0}}^{t_{0} + T} e^{j k Ω_{0} t} d t = 0

otherwise

\int_{t_{0}}^{t_{0} + T} e^{j k Ω_{0} t} d t = \int_{t_{0}}^{t_{0} + T} d t = T

We use [link] to derive an equation for $c_{n}$ as follows. Consider the integral

\int_{t_{0}}^{t_{0} + T} x (t) e^{- j n Ω_{0} t} d t

Substituting the complex form of the Fourier Series of $x (t)$ in [link] , (using $k$ as the index of summation) we obtain

\int_{t_{0}}^{t_{0} + T} [\sum_{k = - \infty}^{\infty}, c_{n}, e^{j k Ω_{0} t}] e^{- j n Ω_{0} t} d t

Rearranging the order of integration and summation, combining the exponents, and using [link] gives

\sum_{k = - \infty}^{\infty} c_{n} \int_{t_{0}}^{t_{0} + T} e^{j (k - n) Ω_{0} t} d t = T c_{n}

Using this result, we find that

c_{n} = \frac{1}{T} \int_{t_{0}}^{t_{0} + T} x (t) e^{- j n Ω_{0} t} d t

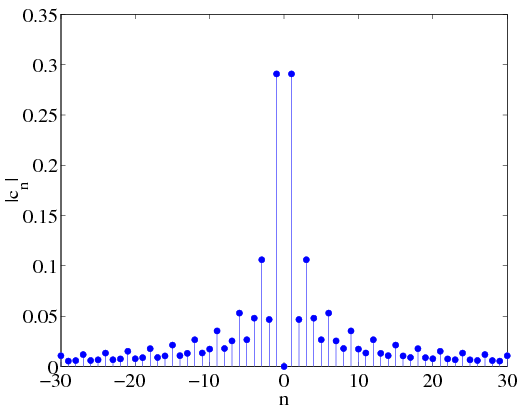
Example 2.1 Let's now find the complex form of the Fourier Series for the signal in Example [link] . The integral to be evaluated is

c_{n} = \frac{2}{3} \int_{- 0.5}^{0.5} 2 t e^{- j \frac{4 π}{3} n t} d t

Integrating by parts yields

c_{n} = \frac{j}{n π} cos (2 π n / 3) - \frac{j 3}{{(n π)}^{2}} sin (2 π n / 3)

[link] shows the magnitude of the coefficients, $|c_{n}|$ . Note that the complex Fourier Series coefficients have even symmetry as was mentioned earlier.

Fourier Series coefficients for Example "Complex Form of the Fourier Series" .

Can the basic formula for computing the $c_{n}$ in [link] be simplified when $x (t)$ has either even, odd, or half-wave symmetry? The answer is yes. We simply use the fact that

c_{n} = \frac{a_{n} - j b_{n}}{2}

and solve for $a_{n}$ and $b_{n}$ using the formulae given above for even, odd, or half-wave symmetric signals. This avoids having to integrate complex quantities. This can also be seen by noting that (setting $t_{0} = T / 2$ in [link] ):

\begin{matrix} c_{n} & = & \frac{1}{T} \int_{- T / 2}^{T / 2} x (t) e^{- j n Ω_{0} t} d t \\ = & \frac{1}{T} \int_{- T / 2}^{T / 2} x (t) cos (n Ω_{0} t) d t - \frac{j}{T} \int_{- T / 2}^{T / 2} x (t) sin (n Ω_{0} t) d t \\ = & \frac{1}{2} a_{n} - \frac{j}{2} b_{n} \end{matrix}

Alternately, if $x (t)$ has half-wave symmetry, we can use [link] , [link] , and [link] to get

c_{n} = \{\begin{matrix} \frac{2}{T} \int_{- T / 4}^{T / 4} x (t) e^{- j n Ω_{0} t} d t, & n odd \\ 0, & n even \end{matrix})

Unlike the trigonometric form, we cannot simplify this further if $x (t)$ is even or odd symmetric since $e^{- j n Ω_{0} t}$ has neither even nor odd symmetry.

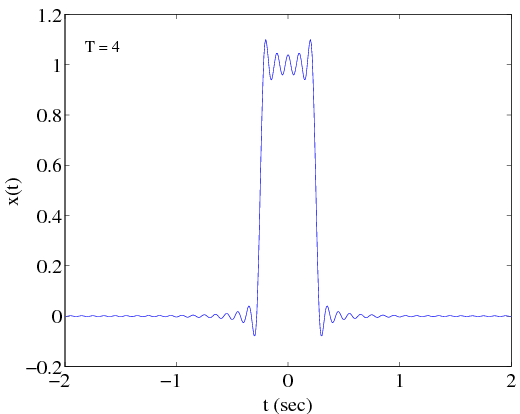
Example 2.2 In this example we will look at the effect of adjusting the period of a pulse train signal. Consider the signal depicted in [link] .

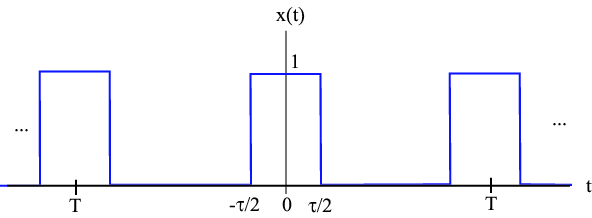
Pulse train having period $T$ used in Example "Complex Form of the Fourier Series" .

The Fourier Series coefficients for this signal are given by

\begin{matrix} c_{n} & = & \frac{1}{T} \int_{- τ / 2}^{τ / 2} e^{- j n Ω_{0} t} d t \\ = & \frac{- 1}{j n Ω_{0} T} (e^{- j n Ω_{0} τ / 2} - e^{j n Ω_{0} τ / 2}) \\ = & \frac{τ}{T} \frac{sin (n Ω_{0} τ / 2)}{n Ω_{0} τ / 2} \\ \equiv & \frac{τ}{T} sinc (n Ω_{0} τ / 2) \end{matrix}

[link] shows the magnitude of $| c_{n} |$ , the amplitude spectrum , for $T = 1$ and $τ = 1 / 2$ as well as the Fourier Series for the signal based on the first 30 coefficients

\hat{x} (t) = \sum_{n = - 30}^{30} c_{n} e^{n Ω_{0} t}

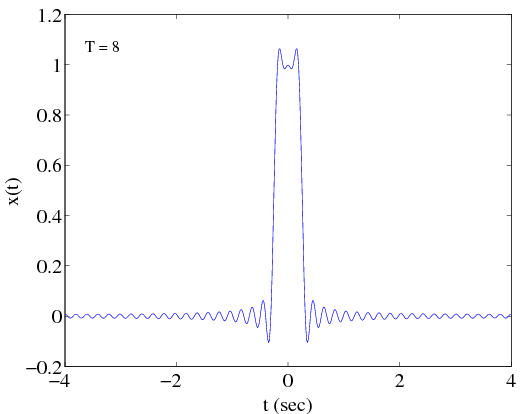
Similar plots are shown in Figures [link] , and [link] , for $T = 4$ , and $T = 8$ , respectively.

Example "Complex Form of the Fourier Series" , $T = 1, τ = 1 / 2$ : (top) Fourier Series coefficient magnitudes, (b) $\hat{x} (t)$ .

Example "Complex Form of the Fourier Series" , $T = 4, τ = 1 / 2$ : (top) Fourier Series coefficient magnitudes, (b) $\hat{x} (t)$ .

Example "Complex Form of the Fourier Series" , $T = 8, τ = 1 / 2$ : (top) Fourier Series coefficient magnitudes, (b) $\hat{x} (t)$ .

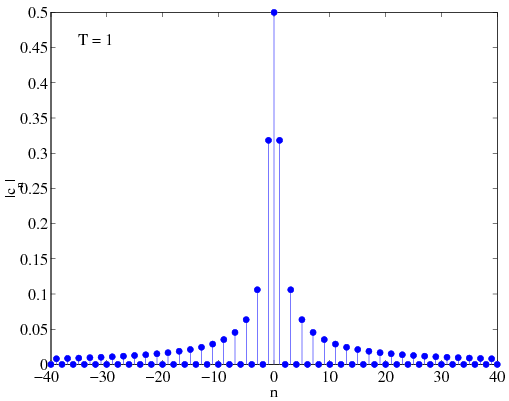
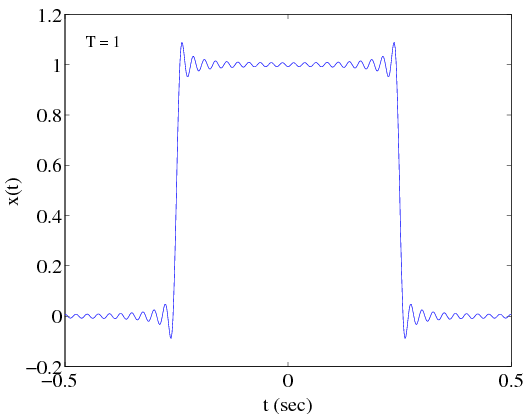
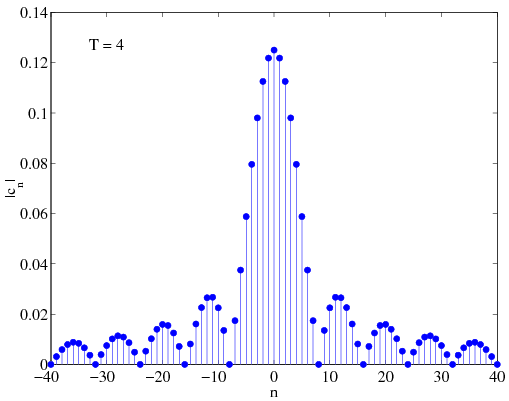
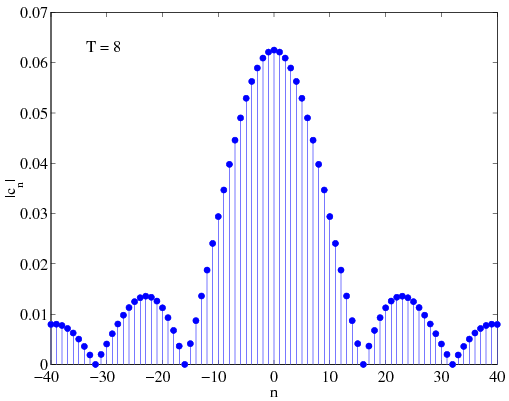
This example illustrates several important points about the Fourier Series: As the period $T$ increases, $Ω_{0}$ decreases in magnitude (this is obvious since $Ω_{0} = 2 π / T$ ). Therefore, as the period increases, successive Fourier Series coefficients represent more closely spaced frequencies. The frequencies corresponding to each $n$ are given by the following table:

$n$	$Ω$
0	0
$\pm 1$	$\pm Ω_{0}$
$\pm 2$	$\pm 2 Ω_{0}$
$⋮$	$⋮$
$\pm n$	$\pm n Ω_{0}$

This table establishes a relation between $n$ and the frequency variable $Ω$ . In particular, if $T = 1$ , we have $Ω_{0} = 2 π$ and

$n$	$Ω$
0	0
$\pm 1$	$\pm 2 π$
$\pm 2$	$\pm 4 π$
$⋮$	$⋮$
$\pm n$	$\pm 2 n π$

If $T = T$ , then $Ω_{0} = π / 2$ and

$n$	$Ω$
0	0
$\pm 1$	$\pm π / 2$
$\pm 2$	$\pm π$
$⋮$	$⋮$
$\pm n$	$\pm n π / 2$

and if $T = 8$ , we have $Ω_{0} = π / 4$ and

$n$	$Ω$
0	0
$\pm 1$	$\pm π / 4$
$\pm 2$	$\pm π / 2$
$⋮$	$⋮$
$\pm n$	$\pm n π / 4$

Note that in all three cases, the first zero coefficient corresponds to the value of $n$ for which $Ω = 4 π$ . Also, as $T$ gets bigger, the $c_{n}$ appear to resemble more closely spaced samples of a continuous function of frequency (since the $n Ω$ are more closely spaced). Can you determine what this function is?

As we shall see, by letting the period $T$ get large (infinitely large), we will derive the Fourier Transform in the next chapter.

References

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Signals, systems, and society. OpenStax CNX. Oct 07, 2012 Download for free at http://cnx.org/content/col10965/1.15

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Signals, systems, and society' conversation and receive update notifications?

Ask

	Autonomic Nervous System By Marriyam Rana Start Quiz
	1 Endocrinology (MCQ) By Rohini Ajay Start Quiz
	13 Dr Garry GI Ruminants quiz By Brooke Delaney Start Exam
	NCE Ch 11 Counseling Families, Diagnosis... By Anh Dao Start Quiz
	2 Week 2 Social Psych By Yacoub Jayoghli Start Quiz
	9 Physiotherapy Modalities By Rhodes Start Exam
	4 AP 04 Tissue Level of Organization MCQ By OpenStax Start Quiz
	4 CDL Quiz - General Knowledge Part 2 By Jazzycazz Jackson Start Quiz
	35 Biology 35 The Nervous System MCQ By OpenStax Start Quiz
	Music 113 By Eric Crawford Start Quiz