| << Chapter < Page | Chapter >> Page > |
Spectrum for finite energy signals
The Fourier integral is intended for non-periodic signals, since the periodicity will lead to problems with the convergence of the integral. In fact, the Fourier integral [link] is defined rigorously only for signals with finite energy (see next section below). Recall that finite energy signals can never be periodic. For an alternative wayof defining for periodic signals see the next bullet just below).
However, in order to make the DFT also useful for non-periodic finite energy signals, we can consider any signal as being restricted to the interval and then extended periodically. Denote this new -periodic signal by with Fourier coefficients . When is large, comparing [link] with [link] gives
The notation instead of should remind the reader, that itself is not periodic.
If not the entire signal but only some samples of the signal are given, we may use the DFT as in [link] and combine it with [link] to get for
Note that this approximation improves in quality as becomes larger; the factor indicates that would have to be made proportionally larger at the same time. For an illustration see [link] , [link] , and [link] , left column, with , . Imagine that we reduce to half, i.e. to , leading to a new signal . This would mean to discard half of the samples, thus leading to . Since the discarded samples are practically zero, using [link] shows that . This agrees with [link] since and .
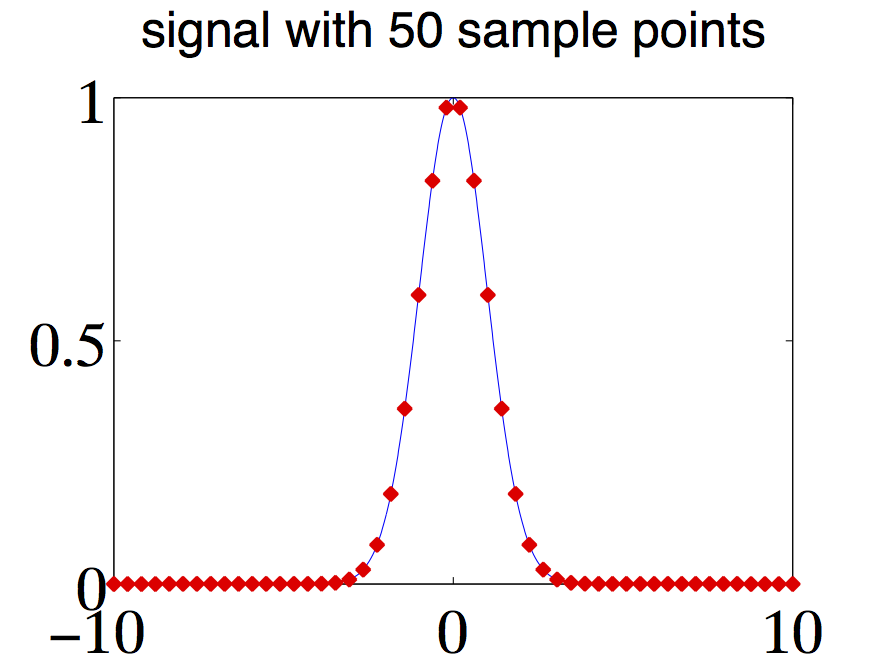
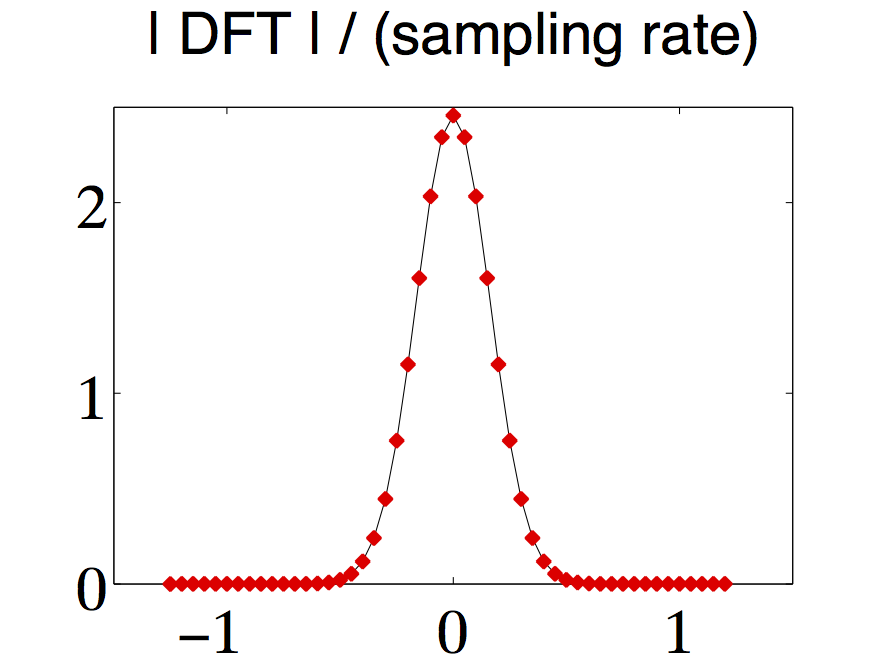
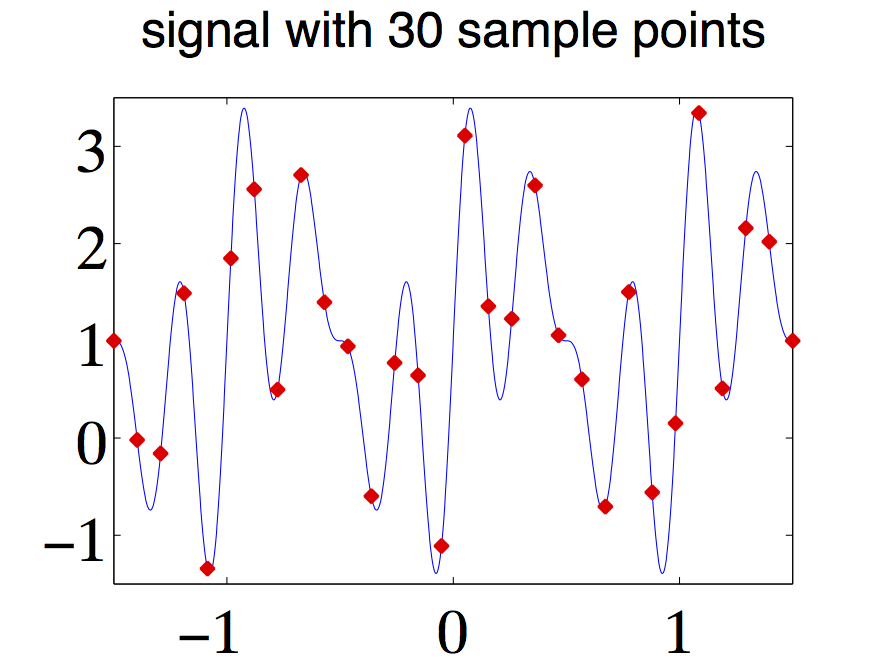
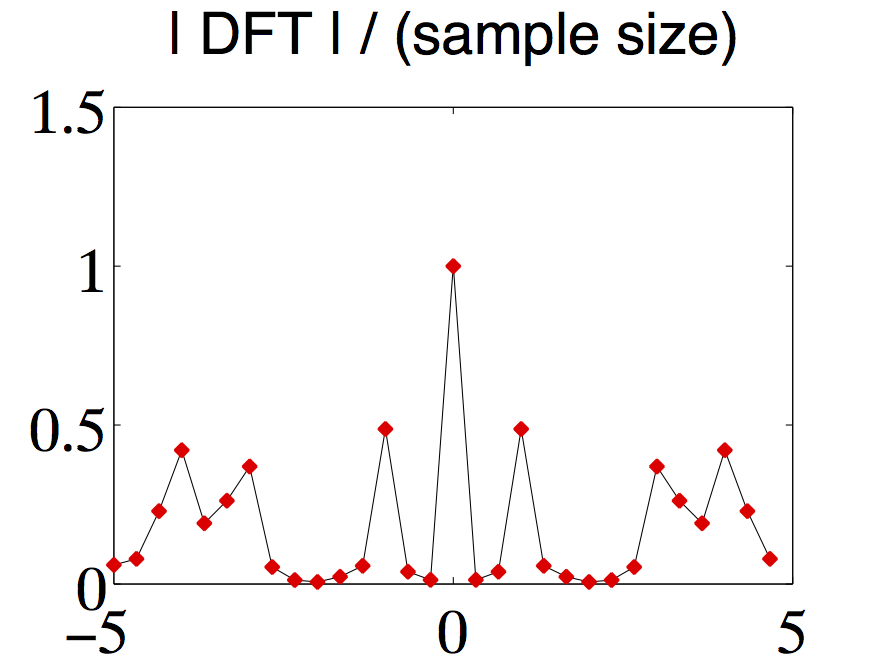
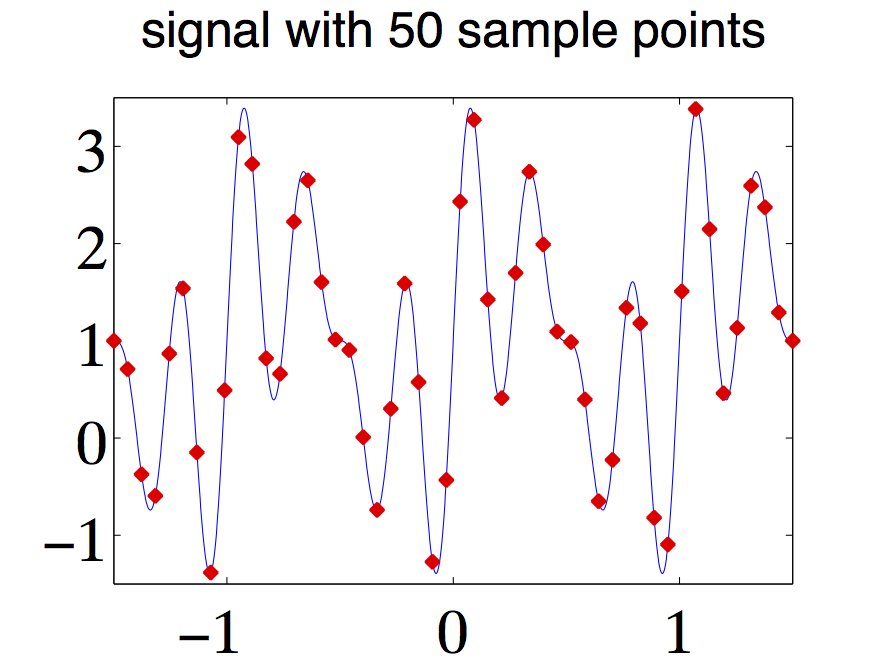
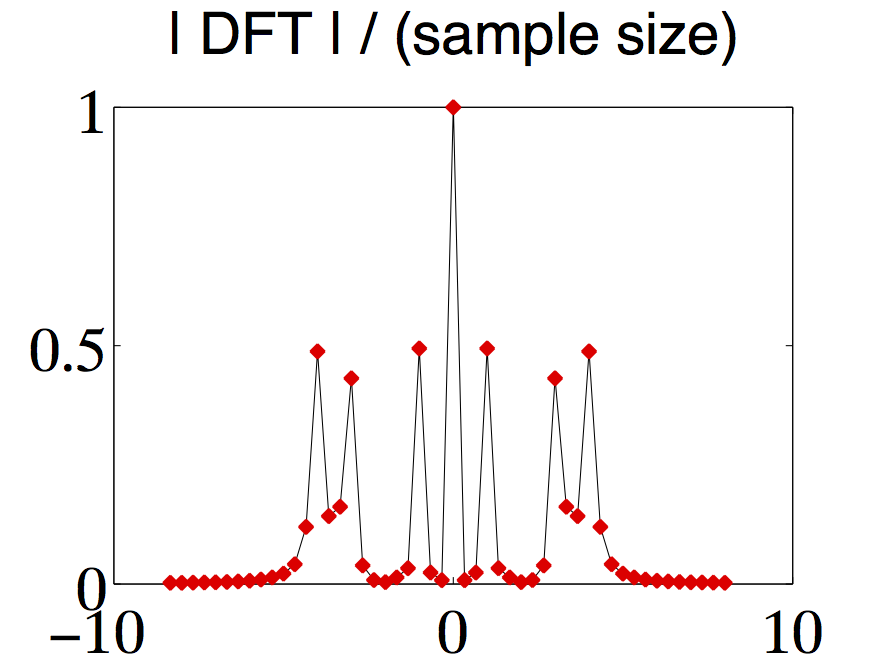
Spectrum for periodic signals
For -periodic signals, the Fourier integral [link] does not converge in the usual sense. One can still define a Fourier transform consisting of Dirac delta functions:
With this setting we have also for periodic signals. Note that the Delta-functions in [link] are “infinitely large” at , in agreement with [link] where should ideally be “infinitely large”.
However, “infinitely large” values are not useful when one wants to read off an amplitude. Comparing [link] and [link] we see that the DFT should be normalized differently for non-periodic finite energy signals than for periodic signals.Dividing the DFT by the sampling rate for non-periodic signals provides an estimation of the Fourier transform via [link] . Dividing the DFT by the sample size for periodic signals provides an estimation of the peak heights of the Dirac delta functionsin [link] (see [link] and [link] ).
Energy and Power from Sampling
First of all, note that the energy of a periodic signal is infinite because there are infinitely many periods with the same energy. On the other hand,the power of a finite energy signal is zero since it is the average energy of an infinitely long interval.
Short, only one measure is meaningful for a signal: either the power or the energy, depending on context. Nevertheless, we may compare power and energy of the various ways of representing asignal: as a finite energy signal, as a signal on a given finite interval (extending it periodically) or through its samples.
Comparing the power of a -periodic signal with its samples over an interval of length , where is an integer multiple of the period , we find in the frequency domain (using [link] and [link] )
Computing in the time domain (using a Riemann Sum) we arrive at the same conclusion:
Comparing the energy for finite energy signals and for their samples on an interval of length we find
where we used [link] in the last step.
In summary, using sufficiently many samples taken over sufficiently large intervalsshould allow to compute the power or energy of signals in either of the three representations, thereby approximating power with energy per time over a long interval.
As an important conclusion we note that the power of a periodic signal should not depend on the number of samples taken, at least approximatively, and as long as sufficient many samplesare taken. We will later make precise how many samples are sufficient. Similar for the energy of a finite energy signal.
As a final remark we note that the name “power spectrum” used for , and is appropriate since they indicate how the power is distributed of the spectrum of frequencies, i.e., which frequencies contribute much and which less to the power.

Notification Switch
Would you like to follow the 'Sampling rate conversion' conversation and receive update notifications?