| << Chapter < Page | Chapter >> Page > |
Use the first derivative test to locate all local extrema for
has a local minimum at and a local maximum at
Use the first derivative test to find the location of all local extrema for Use a graphing utility to confirm your results.
Step 1. The derivative is
The derivative when Therefore, at The derivative is undefined at Therefore, we have three critical points: and Consequently, divide the interval into the smaller intervals and
Step 2: Since is continuous over each subinterval, it suffices to choose a test point in each of the intervals from step and determine the sign of at each of these points. The points are test points for these intervals.
| Interval | Test Point | Sign of at Test Point | Conclusion |
|---|---|---|---|
| is decreasing. | |||
| is increasing. | |||
| is increasing. | |||
| is decreasing. |
Step 3: Since is decreasing over the interval and increasing over the interval has a local minimum at Since is increasing over the interval and the interval does not have a local extremum at Since is increasing over the interval and decreasing over the interval has a local maximum at The analytical results agree with the following graph.
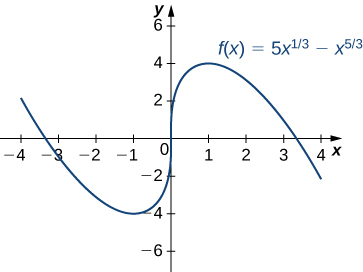
Use the first derivative test to find all local extrema for
has no local extrema because does not change sign at
We now know how to determine where a function is increasing or decreasing. However, there is another issue to consider regarding the shape of the graph of a function. If the graph curves, does it curve upward or curve downward? This notion is called the concavity of the function.
[link] (a) shows a function with a graph that curves upward. As increases, the slope of the tangent line increases. Thus, since the derivative increases as increases, is an increasing function. We say this function is concave up. [link] (b) shows a function that curves downward. As increases, the slope of the tangent line decreases. Since the derivative decreases as increases, is a decreasing function. We say this function is concave down.
Let be a function that is differentiable over an open interval If is increasing over we say is concave up over If is decreasing over we say is concave down over
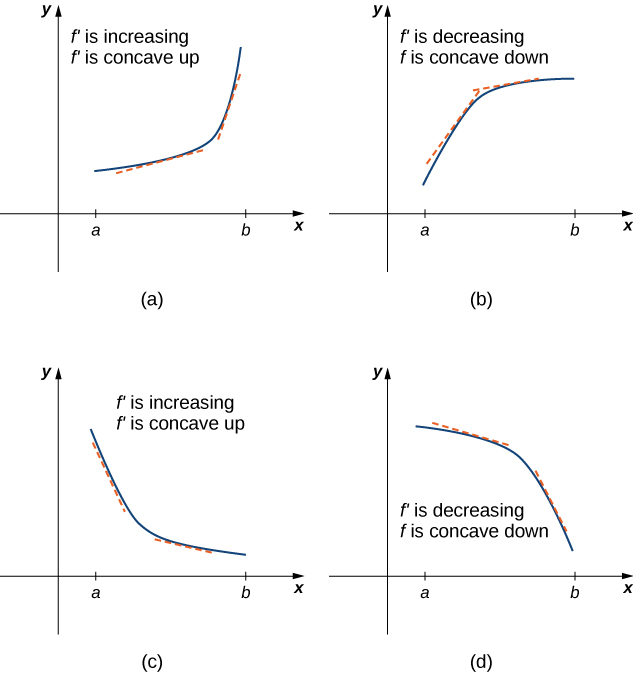
In general, without having the graph of a function how can we determine its concavity? By definition, a function is concave up if is increasing. From Corollary we know that if is a differentiable function, then is increasing if its derivative Therefore, a function that is twice differentiable is concave up when Similarly, a function is concave down if is decreasing. We know that a differentiable function is decreasing if its derivative Therefore, a twice-differentiable function is concave down when Applying this logic is known as the concavity test .

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?