7.6 Quadratic equations (Page 5/9)

Page 5 / 9

A rectangular sign has area 30 square feet. The length of the sign is one foot more than the width. Find the length and width of the sign.

$5$ feet and $6$ feet

Got questions? Get instant answers now!

A rectangular patio has area 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.

$12$ feet and $15$ feet

Got questions? Get instant answers now!

In an earlier chapter, we used the Pythagorean Theorem $(a^{2} + b^{2} = c^{2})$ . It gave the relation between the legs and the hypotenuse of a right triangle.

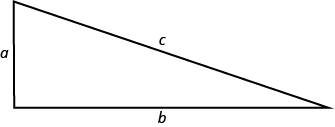
We will use this formula to in the next example.

Justine wants to put a deck in the corner of her backyard in the shape of a right triangle, as shown below. The hypotenuse will be 17 feet long. The length of one side will be 7 feet less than the length of the other side. Find the lengths of the sides of the deck.

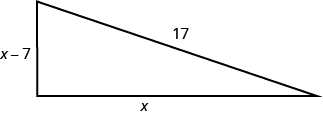
This figure is a right triangle. The vertical leg is labeled “x – 7”. the horizontal leg, the base, is labeled “x”. The hypotenuse is labeled “17”.

Solution

This image shows the steps for solving the above deck problem. The first step is reading the problem. The second step is identify what you are looking for, which is the lengths of the sides of the deck. The third step is naming what you are looking for, which is x = length of one side of the deck and x – 7 the length of the other side. The fourth step is translating into an equation. This problem uses the Pythagorean theorem, x squared + (x – 7) squared = 17 squared. The fifth step is to simplify the equation and solve. The equation simplifies to 2 x squared – 14 x + 49 = 289. Then, the equation is put into standard quadratic form, 2 x squared – 14 x – 240 = 0. The equation is then factored into 2 (x – 15)(x + 8) = 0. Each factor is set equal to 0 and solved, x = 15 or x = −8. Since x = negative 8 does not make sense, the solution is x = 15. The sixth step is to see if the answer makes sense. The last step is to answer the question, the sides of the deck are 8, 15, and 17 feet.

Step 1. Read the problem.
Step 2. Identify what you are looking for.	We are looking for the lengths of the sides of the deck.
Step 3. Name what you are looking for. One side is 7 less than the other.	Let x = length of a side of the deck x − 7 = length of other side
Step 4. Translate into an equation. Since this is a right triangle we can use the Pythagorean Theorem.	$a^{2} + b^{2} = c^{2}$
Substitute in the variables.	$x^{2} + {(x - 7)}^{2} = 17^{2}$
Step 5. Solve the equation.	$x^{2} + x^{2} - 14 x + 49 = 289$
Simplify.	$2 x^{2} - 14 x + 49 = 289$
It is a quadratic equation, so get zero on one side.	$2 x^{2} - 14 x - 240 = 0$
Factor the greatest common factor.	$2 (x^{2} - 7 x - 120) = 0$
Factor the trinomial.	$2 (x - 15) (x + 8) = 0$
Use the Zero Product Property.	$2 \neq 0$	$x - 15 = 0$	$x + 8 = 0$
Solve.	$2 \neq 0$	$x = 15$	$x = −8$
Since x is a side of the triangle, $x = −8$ does not make sense.	$2 \neq 0$	$x = 15$	$x = −8$
Find the length of the other side.
If the length of one side is
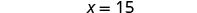then the length of the other side is

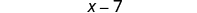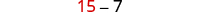	8 is the length of the other side.
Step 6. Check the answer. Do these numbers make sense?

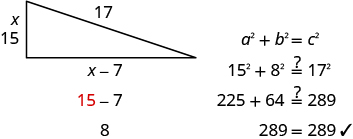Step 7. Answer the question.	The sides of the deck are 8, 15, and 17 feet.

Got questions? Get instant answers now!

A boat’s sail is a right triangle. The length of one side of the sail is 7 feet more than the other side. The hypotenuse is 13. Find the lengths of the two sides of the sail.

$5$ feet and $12$ feet

Got questions? Get instant answers now!

A meditation garden is in the shape of a right triangle, with one leg 7 feet. The length of the hypotenuse is one more than the length of one of the other legs. Find the lengths of the hypotenuse and the other leg.

$24$ feet and $25$ feet

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 2

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Elementary algebra. OpenStax CNX. Jan 18, 2017 Download for free at http://cnx.org/content/col12116/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Elementary algebra' conversation and receive update notifications?

Ask

	MAPEH Test G9 (Physical Education) By Angelica Lito Start Quiz
	Social Media By Brenna Fike Start Quiz
	Vocabulary Week 1-3 By Rachel Woolard Start Quiz
©flickr: Francisco	U.S. Civil War Pre-test By Danielle Stephens Start Quiz
	6 Microeconomics 06 Elasticity By OpenStax Start Flashcards
	5 Sociology 05 Socialization MCQ By OpenStax Start Quiz
	Anthropology Environment, Adaption Subsistence By Richley Crapo Start Assignment
	Cultural Evolution Contemporary World By Richley Crapo Start Assignment
	23 AP 23 Digestive System MCQ By OpenStax Start Quiz
©flickr:	Anatomy Physiology By Jemekia Weeden Start Quiz