7.3 Factor quadratic trinomials with leading coefficient other than (Page 3/6)

Elementary algebra Page 3 / 6

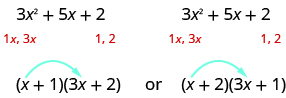
This figure demonstrates the possible factors of the polynomial 3x^2 +5x +2. The polynomial is written twice. Underneath both, there are the terms 1x, 3x under the 3x^2. Also, there are the factors 1,2 under the 2 term. At the bottom of the figure there are two possible factorizations of the polynomial. The first is (x + 1)(3x + 2) and the next is (x + 2)(3x + 1).

Which factors are correct? To decide that, we multiply the inner and outer terms.

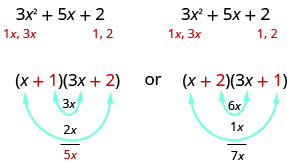
Since the middle term of the trinomial is 5 x , the factors in the first case will work. Let’s FOIL to check.

\begin{matrix} (x + 1) (3 x + 2) \\ 3 x^{2} + 2 x + 3 x + 2 \\ 3 x^{2} + 5 x + 2 ✓ \end{matrix}

Our result of the factoring is:

\begin{matrix} 3 x^{2} + 5 x + 2 \\ (x + 1) (3 x + 2) \end{matrix}

How to factor trinomials of the form $a x^{2} + b x + c$ Using trial and error

Factor completely: $3 y^{2} + 22 y + 7$ .

Solution

This table summarizes the steps for factoring 3 y ^ 2 + 22 y + 7. The first row states write the trinomial in descending order. The polynomial is written 3 y ^ 2 +22 y + 7.

The second row states find all the factor pairs of the first term. The only pairs listed are 1 y, 3 y. Then, since there is only one pair, they are in the parentheses written (1 y ) and (3 y ).

The third row states “find all the factored pairs of the third term”. It also states the only factors of 7 are 1 and 7.

The fourth row states test all the possible combinations of the factors until the correct product is found. The possible factors are shown (y + 1)(3 y + 7) and (y + 7)(3y + 1). Under each factor is the products of the outer terms and the inner terms. For the first it is 7y and 3y. For the second it is 21 y and y. The combination (y + 7)(3 y + 1) is the correct factoring.

The last row states to check by multiplying. The product of (y + 7)(3 y + 1) is shown as 3 y ^ 2 + 22 y + 7.

Got questions? Get instant answers now!

Factor completely: $2 a^{2} + 5 a + 3$ .

$(a + 1) (2 a + 3)$

Got questions? Get instant answers now!

Factor completely: $4 b^{2} + 5 b + 1$ .

$(b + 1) (4 b + 1)$

Got questions? Get instant answers now!

Factor trinomials of the form $a x^{2} + b x + c$ Using trial and error.

Write the trinomial in descending order of degrees.
Find all the factor pairs of the first term.
Find all the factor pairs of the third term.
Test all the possible combinations of the factors until the correct product is found.
Check by multiplying.

When the middle term is negative and the last term is positive, the signs in the binomials must both be negative.

Factor completely: $6 b^{2} - 13 b + 5$ .

Solution

The trinomial is already in descending order.
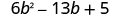Find the factors of the first term.
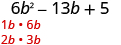Find the factors of the last term. Consider the signs. Since the last term, 5 is positive its factors must both be positive or both be negative. The coefficient of the middle term is negative, so we use the negative factors.

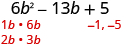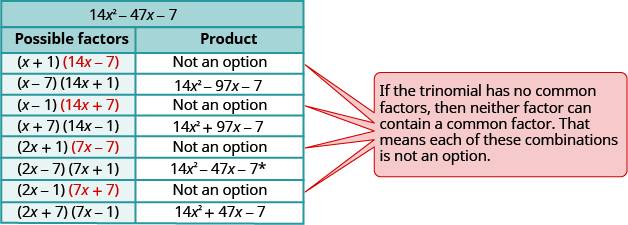
Consider all the combinations of factors.

$6 b^{2} - 13 b + 5$
Possible factors	Product
$(b - 1) (6 b - 5)$	$6 b^{2} - 11 b + 5$
$(b - 5) (6 b - 1)$	$6 b^{2} - 31 b + 5$
$(2 b - 1) (3 b - 5)$	$6 b^{2} - 13 b + 5$ *
$(2 b - 5) (3 b - 1)$	$6 b^{2} - 17 b + 5$

$\begin{matrix} The correct factors are those whose product \\ is the original trinomial. & (2 b - 1) (3 b - 5) \\ Check by multiplying. \\ (2 b - 1) (3 b - 5) \\ 6 b^{2} - 10 b - 3 b + 5 \\ 6 b^{2} - 13 b + 5 ✓ \end{matrix}$

Got questions? Get instant answers now!

Factor completely: $8 x^{2} - 13 x + 3$ .

$(2 x - 3) (4 x - 1)$

Got questions? Get instant answers now!

Factor completely: $10 y^{2} - 37 y + 7$ .

$(2 y - 7) (5 y - 1)$

Got questions? Get instant answers now!

When we factor an expression, we always look for a greatest common factor first. If the expression does not have a greatest common factor, there cannot be one in its factors either. This may help us eliminate some of the possible factor combinations.

Factor completely: $14 x^{2} - 47 x - 7$ .

Solution

The trinomial is already in descending order.
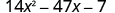Find the factors of the first term.
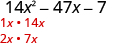Find the factors of the last term. Consider the signs. Since it is negative, one factor must be positive and one negative.

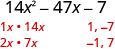Consider all the combinations of factors. We use each pair of the factors of $14 x^{2}$ with each pair of factors of $−7 .$

Factors of $14 x^{2}$	Pair with	Factors of $−7$
$x$ , $14 x$		$1$ , $−7$ $−7$ , $1$ (reverse order)
$x$ , $14 x$		$−1$ , $7$ $7$ , $−1$ (reverse order)
$2 x, 7 x$		$1$ , $−7$ $−7$ , $1$ (reverse order)
$2 x, 7 x$		$−1$ , $7$ $7$ , $−1$ (reverse order)

These pairings lead to the following eight combinations.

This table has the heading 14 x ^ 2 – 47 x minus 7. This table has two columns. The first column is labeled “possible factors” and the second column is labeled “product”. The first column lists all the combinations of possible factors and the second column has the products. In the first row under “possible factors” it reads (x+1) and (14 x minus 7). Under product, in the next column, it says “not an option”. In the next row down, it shows (x minus 7) and (14 x plus 1). In the next row down, it shows (x minus 1) and (14 x plus 7). Next to this in the product column, it says “not an option.” The next row down under “possible factors”, it has the equation (x plus 7 and 14 x minus 1. Next to this in the product column it has 14 x ^2 plus 97 x minus 7. The next row down under possible factors, it has 2 x plus 1 and 7 x minus 7. Next to this under the product column, is says “not an option”. The next row down reads 2 x minus 7 and 7x plus 1. Next to this under the product column, it has 14 x ^2 minus 47 x minus 7 with the asterisk following the 7. The next row down reads 2 x minus 1 and 7 x plus 7. Next to this in the product column it reads “not an option”. The final row reads 2 x plus 7 and 7 x minus 1. Next to this in the product column it reads 14, x, ^ 2 plus 47 x minus 7. Next to the table is a box with four arrows point to each “not an option” row. The reason given in the textbox is “if the trinomial has no common factors, then neither factor can contain a common factor. That means that each of these combinations is not an option.”

$\begin{matrix} The correct factors are those whose product is the & (2 x - 7) (7 x + 1) \\ original trinomial. \\ Check by multiplying. \\ (2 x - 7) (7 x + 1) \\ 14 x^{2} + 2 x - 49 x - 7 \\ 14 x^{2} - 47 x - 7 ✓ \end{matrix}$

Got questions? Get instant answers now!

Factor completely: $8 a^{2} - 3 a - 5$ .

$(a - 1) (8 a + 5)$

Got questions? Get instant answers now!

Factor completely: $6 b^{2} - b - 15$ .

$(2 b + 3) (3 b - 5)$

Got questions? Get instant answers now!

Factor completely: $18 n^{2} - 37 n + 15$ .

Solution

The trinomial is already in descending order.	$18 n^{2} - 37 n + 15$
Find the factors of the first term.
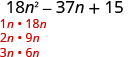Find the factors of the last term. Consider the signs. Since 15 is positive and the coefficient of the middle term is negative, we use the negative facotrs.

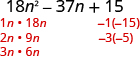Consider all the combinations of factors.

$\begin{matrix} The correct factors are those whose product is & (2 n - 3) (9 n - 5) \\ the original trinomial. \\ Check by multiplying. \\ (2 n - 3) (9 n - 5) \\ 18 n^{2} - 10 n - 27 n + 15 \\ 18 n^{2} - 37 n + 15 ✓ \end{matrix}$

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 1

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Elementary algebra. OpenStax CNX. Jan 18, 2017 Download for free at http://cnx.org/content/col12116/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Elementary algebra' conversation and receive update notifications?

Ask

	3 Understanding Societies MCQ By Jessica Collett Start Quiz
	3 Pharmacology Excl. Nervous System MCQ By Rohini Ajay Start Quiz
	14 AP Key Terms 14 Brain Cranial Nerves By OpenStax Start Key Terms
	2 Biology 02 The Chemical Foundation of Life MCQ By OpenStax Start Quiz
	23 AP 23 Digestive System Essay By OpenStax Start Flashcards
	College physics By OpenStax Read Online Course
	25 AP Key Terms 25 The Urinary System By OpenStax Start Key Terms
	37 Biology 37 The Endocrine System MCQ By OpenStax Start Quiz
©flickr: Alexander	Mechanics I MCQ By Stephanie Redfern Start Quiz
©flickr:	Dairy Cattle Evaluation Exam By Katy Keilers Start Exam

7.3 Factor quadratic trinomials with leading coefficient other than (Page 3/6)

How to factor trinomials of the form a x 2 + b x + c Using trial and error

Solution

Factor trinomials of the form a x 2 + b x + c Using trial and error.

Solution

Solution

Solution

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

How to factor trinomials of the form $a x^{2} + b x + c$ Using trial and error

Factor trinomials of the form $a x^{2} + b x + c$ Using trial and error.