| << Chapter < Page | Chapter >> Page > |
Recognize the Relation Between the Solutions of an Equation and its Graph
In the following exercises, for each ordered pair, decide:
Graph a Linear Equation by Plotting Points
In the following exercises, graph by plotting points.
Graph Vertical and Horizontal lines
In the following exercises, graph each equation.
In the following exercises, graph each pair of equations in the same rectangular coordinate system.
Identify the x - and y -Intercepts on a Graph
In the following exercises, find the x - and y -intercepts.
Find the x - and y -Intercepts from an Equation of a Line
In the following exercises, find the intercepts of each equation.
Graph a Line Using the Intercepts
In the following exercises, graph using the intercepts.
Use Geoboards to Model Slope
In the following exercises, find the slope modeled on each geoboard.
In the following exercises, model each slope. Draw a picture to show your results.
Use to find the Slope of a Line from its Graph
In the following exercises, find the slope of each line shown.
Find the Slope of Horizontal and Vertical Lines
In the following exercises, find the slope of each line.
Use the Slope Formula to find the Slope of a Line between Two Points
In the following exercises, use the slope formula to find the slope of the line between each pair of points.
Graph a Line Given a Point and the Slope
In the following exercises, graph each line with the given point and slope.
x -intercept ;
Solve Slope Applications
In the following exercises, solve these slope applications.
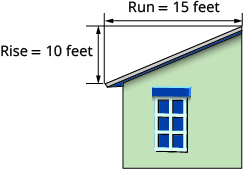
The roof pictured below has a rise of 10 feet and a run of 15 feet. What is its slope?
A mountain road rises 50 feet for a 500-foot run. What is its slope?
Recognize the Relation Between the Graph and the Slope–Intercept Form of an Equation of a Line
In the following exercises, use the graph to find the slope and y -intercept of each line. Compare the values to the equation .
Identify the Slope and y-Intercept from an Equation of a Line
In the following exercises, identify the slope and y -intercept of each line.
Graph a Line Using Its Slope and Intercept
In the following exercises, graph the line of each equation using its slope and y -intercept.
In the following exercises, determine the most convenient method to graph each line.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?