| << Chapter < Page | Chapter >> Page > |
A jetliner changes altitude as its distance from the starting point of a flight increases. The weight of a growing child increases with time. In each case, one quantity depends on another. There is a relationship between the two quantities that we can describe, analyze, and use to make predictions. In this section, we will analyze such relationships.
A relation is a set of ordered pairs. The set of the first components of each ordered pair is called the domain and the set of the second components of each ordered pair is called the range . Consider the following set of ordered pairs. The first numbers in each pair are the first five natural numbers. The second number in each pair is twice that of the first.
The domain is The range is
Note that each value in the domain is also known as an input value, or independent variable , and is often labeled with the lowercase letter Each value in the range is also known as an output value, or dependent variable , and is often labeled lowercase letter
A function is a relation that assigns a single value in the range to each value in the domain . In other words, no x -values are repeated. For our example that relates the first five natural numbers to numbers double their values, this relation is a function because each element in the domain, is paired with exactly one element in the range,
Now let’s consider the set of ordered pairs that relates the terms “even” and “odd” to the first five natural numbers. It would appear as
Notice that each element in the domain, is not paired with exactly one element in the range, For example, the term “odd” corresponds to three values from the domain, and the term “even” corresponds to two values from the range, This violates the definition of a function, so this relation is not a function.
[link] compares relations that are functions and not functions.
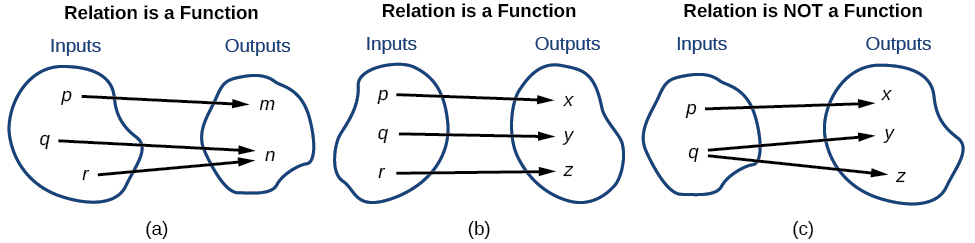
A function is a relation in which each possible input value leads to exactly one output value. We say “the output is a function of the input.”
The input values make up the domain , and the output values make up the range .
Given a relationship between two quantities, determine whether the relationship is a function.

Notification Switch
Would you like to follow the 'Essential precalculus, part 1' conversation and receive update notifications?