| << Chapter < Page | Chapter >> Page > |
The next expansion would be
But where do those coefficients come from? The binomial coefficients are symmetric. We can see these coefficients in an array known as Pascal's Triangle , shown in [link] .
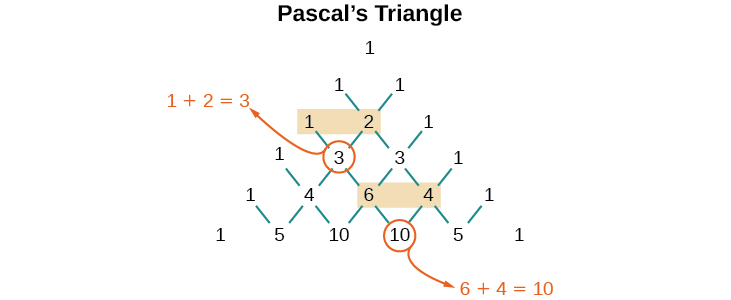
To generate Pascal’s Triangle, we start by writing a 1. In the row below, row 2, we write two 1’s. In the 3 rd row, flank the ends of the rows with 1’s, and add to find the middle number, 2. In the row, flank the ends of the row with 1’s. Each element in the triangle is the sum of the two elements immediately above it.
To see the connection between Pascal’s Triangle and binomial coefficients, let us revisit the expansion of the binomials in general form.
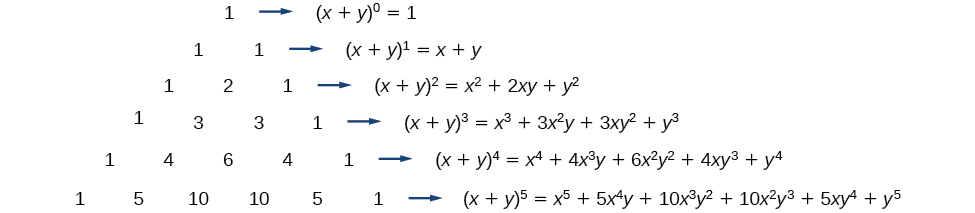
The Binomial Theorem is a formula that can be used to expand any binomial.
Given a binomial, write it in expanded form.
Write in expanded form.
Expanding a binomial with a high exponent such as can be a lengthy process.
Sometimes we are interested only in a certain term of a binomial expansion. We do not need to fully expand a binomial to find a single specific term.
Note the pattern of coefficients in the expansion of
The second term is The third term is We can generalize this result.
The term of the binomial expansion of is:
Given a binomial, write a specific term without fully expanding.
Find the tenth term of without fully expanding the binomial.
Because we are looking for the tenth term, we will use in our calculations.
Find the sixth term of without fully expanding the binomial.
Access these online resources for additional instruction and practice with binomial expansion.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?