| << Chapter < Page | Chapter >> Page > |
Dropping a perpendicular from the point in the plane to the x- axis forms a right triangle, as illustrated in [link] . An easy way to remember the equations above is to think of as the adjacent side over the hypotenuse and as the opposite side over the hypotenuse.
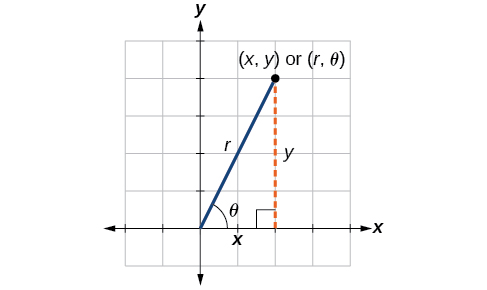
To convert polar coordinates to rectangular coordinates let
Given polar coordinates, convert to rectangular coordinates.
Write the polar coordinates as rectangular coordinates.
Write the polar coordinates as rectangular coordinates.
See [link] . Writing the polar coordinates as rectangular, we have
The rectangular coordinates are also
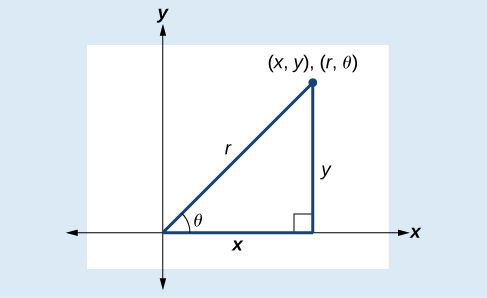
To convert rectangular coordinates to polar coordinates , we will use two other familiar relationships. With this conversion, however, we need to be aware that a set of rectangular coordinates will yield more than one polar point.
Converting from rectangular coordinates to polar coordinates requires the use of one or more of the relationships illustrated in [link] .
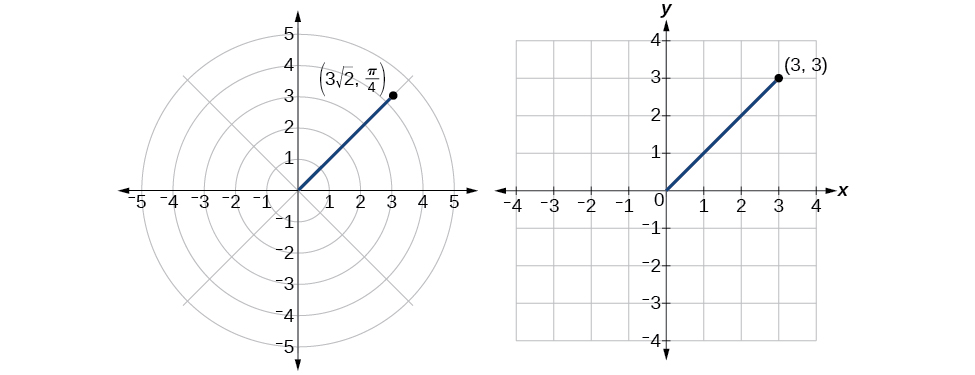
Convert the rectangular coordinates to polar coordinates.
We see that the original point is in the first quadrant. To find use the formula This gives
To find we substitute the values for and into the formula We know that must be positive, as is in the first quadrant. Thus
So, and giving us the polar point See [link] .
We can now convert coordinates between polar and rectangular form. Converting equations can be more difficult, but it can be beneficial to be able to convert between the two forms. Since there are a number of polar equations that cannot be expressed clearly in Cartesian form, and vice versa, we can use the same procedures we used to convert points between the coordinate systems. We can then use a graphing calculator to graph either the rectangular form or the polar form of the equation.
Given an equation in polar form, graph it using a graphing calculator.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?