| << Chapter < Page | Chapter >> Page > |
Rewrite the polar equation as a Cartesian equation.
The goal is to eliminate and and introduce and We clear the fraction, and then use substitution. In order to replace with and we must use the expression
The Cartesian equation is However, to graph it, especially using a graphing calculator or computer program, we want to isolate
When our entire equation has been changed from and to and we can stop, unless asked to solve for or simplify. See [link] .
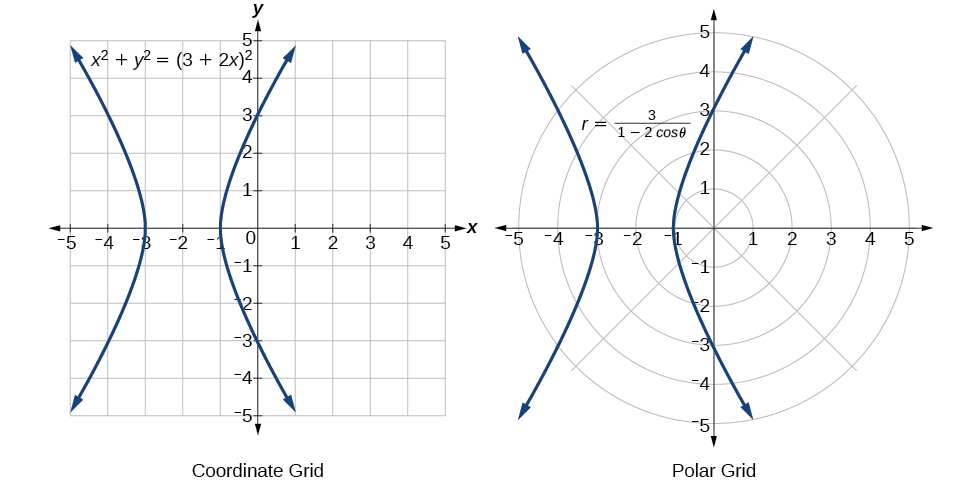
The “hour-glass” shape of the graph is called a hyperbola . Hyperbolas have many interesting geometric features and applications, which we will investigate further in Analytic Geometry .
Rewrite the polar equation in Cartesian form.
or, in the standard form for a circle,
Rewrite the polar equation in Cartesian form.
This equation can also be written as
Access these online resources for additional instruction and practice with polar coordinates.
| Conversion formulas |
How are polar coordinates different from rectangular coordinates?
For polar coordinates, the point in the plane depends on the angle from the positive x- axis and distance from the origin, while in Cartesian coordinates, the point represents the horizontal and vertical distances from the origin. For each point in the coordinate plane, there is one representation, but for each point in the polar plane, there are infinite representations.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?