| << Chapter < Page | Chapter >> Page > |
If division of a polynomial by a binomial results in a remainder of zero, what can be conclude?
The binomial is a factor of the polynomial.
If a polynomial of degree is divided by a binomial of degree 1, what is the degree of the quotient?
For the following exercises, use long division to divide. Specify the quotient and the remainder.
For the following exercises, use synthetic division to find the quotient.
For the following exercises, use synthetic division to determine whether the first expression is a factor of the second. If it is, indicate the factorization.
For the following exercises, use the graph of the third-degree polynomial and one factor to write the factored form of the polynomial suggested by the graph. The leading coefficient is one.
Factor is
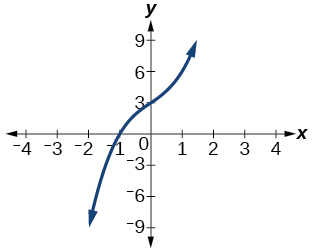
Factor is
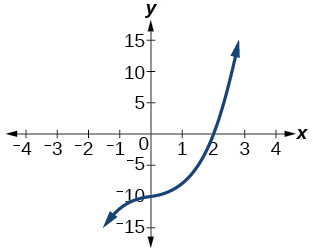
Factor is
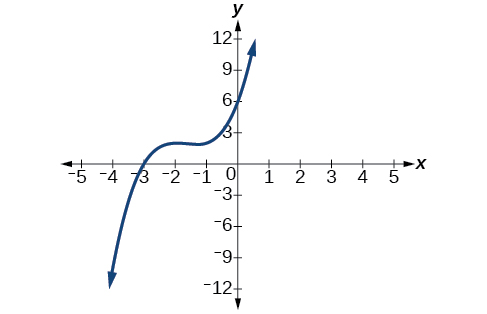
For the following exercises, use synthetic division to find the quotient and remainder.
For the following exercises, use a calculator with CAS to answer the questions.
Consider with What do you expect the result to be if
Consider for What do you expect the result to be if
Consider with What do you expect the result to be if
For the following exercises, use synthetic division to determine the quotient involving a complex number.
For the following exercises, use the given length and area of a rectangle to express the width algebraically.
Length is area is
Length is area is
For the following exercises, use the given volume of a box and its length and width to express the height of the box algebraically.
Volume is length is width is
Volume is length is width is
For the following exercises, use the given volume and radius of a cylinder to express the height of the cylinder algebraically.
Volume is radius is

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?