| << Chapter < Page | Chapter >> Page > |
Solve the rational equation after factoring the denominators: State the excluded values.
We must factor the denominator We recognize this as the difference of squares, and factor it as Thus, the LCD that contains each denominator is Multiply the whole equation by the LCD, cancel out the denominators, and solve the remaining equation.
The solution is The excluded values are and
Perhaps the most familiar form of a linear equation is the slope-intercept form, written as where and Let us begin with the slope.
The slope of a line refers to the ratio of the vertical change in y over the horizontal change in x between any two points on a line. It indicates the direction in which a line slants as well as its steepness. Slope is sometimes described as rise over run.
If the slope is positive, the line slants to the right. If the slope is negative, the line slants to the left. As the slope increases, the line becomes steeper. Some examples are shown in [link] . The lines indicate the following slopes: and
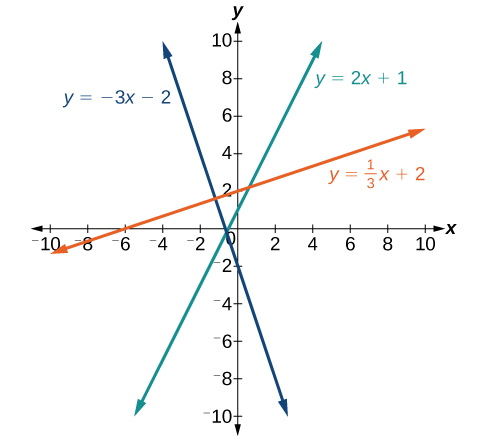
The slope of a line, m , represents the change in y over the change in x. Given two points, and the following formula determines the slope of a line containing these points:
Find the slope of a line that passes through the points and
We substitute the y- values and the x- values into the formula.
The slope is
Find the slope of the line that passes through the points and
Identify the slope and y- intercept, given the equation
As the line is in form, the given line has a slope of The y- intercept is
Given the slope and one point on a line, we can find the equation of the line using the point-slope formula.
This is an important formula, as it will be used in other areas of college algebra and often in calculus to find the equation of a tangent line. We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we simplify it and write it in slope-intercept form.
Given one point and the slope, the point-slope formula will lead to the equation of a line:
Write the equation of the line with slope and passing through the point Write the final equation in slope-intercept form.
Using the point-slope formula, substitute for m and the point for

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?