| << Chapter < Page | Chapter >> Page > |
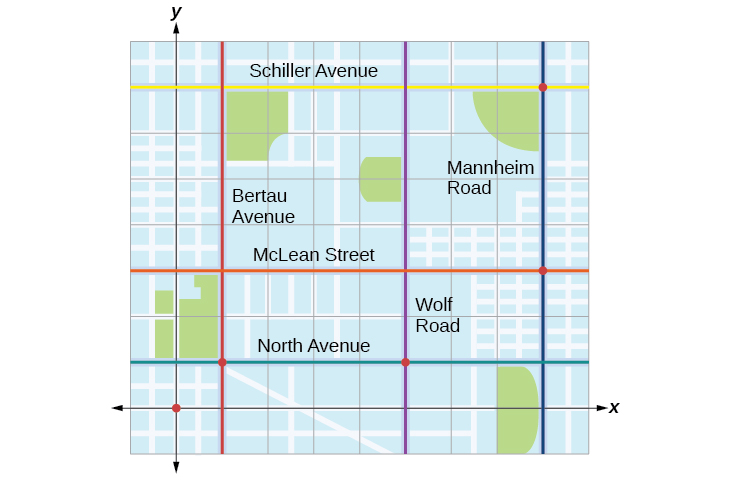
Tracie set out from Elmhurst, IL, to go to Franklin Park. On the way, she made a few stops to do errands. Each stop is indicated by a red dot in [link] . Laying a rectangular coordinate grid over the map, we can see that each stop aligns with an intersection of grid lines. In this section, we will learn how to use grid lines to describe locations and changes in locations.
An old story describes how seventeenth-century philosopher/mathematician René Descartes invented the system that has become the foundation of algebra while sick in bed. According to the story, Descartes was staring at a fly crawling on the ceiling when he realized that he could describe the fly’s location in relation to the perpendicular lines formed by the adjacent walls of his room. He viewed the perpendicular lines as horizontal and vertical axes. Further, by dividing each axis into equal unit lengths, Descartes saw that it was possible to locate any object in a two-dimensional plane using just two numbers—the displacement from the horizontal axis and the displacement from the vertical axis.
While there is evidence that ideas similar to Descartes’ grid system existed centuries earlier, it was Descartes who introduced the components that comprise the Cartesian coordinate system , a grid system having perpendicular axes. Descartes named the horizontal axis the x- axis and the vertical axis the y- axis .
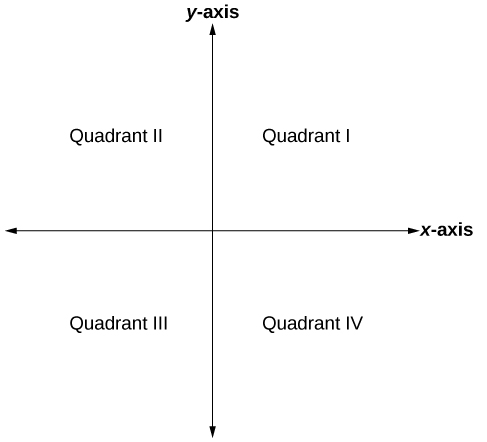
The Cartesian coordinate system, also called the rectangular coordinate system, is based on a two-dimensional plane consisting of the x -axis and the y -axis. Perpendicular to each other, the axes divide the plane into four sections. Each section is called a quadrant ; the quadrants are numbered counterclockwise as shown in [link]
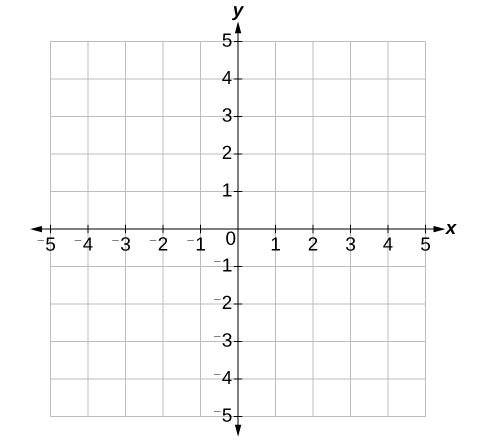
The center of the plane is the point at which the two axes cross. It is known as the origin , or point From the origin, each axis is further divided into equal units: increasing, positive numbers to the right on the x- axis and up the y- axis; decreasing, negative numbers to the left on the x- axis and down the y- axis. The axes extend to positive and negative infinity as shown by the arrowheads in [link] .
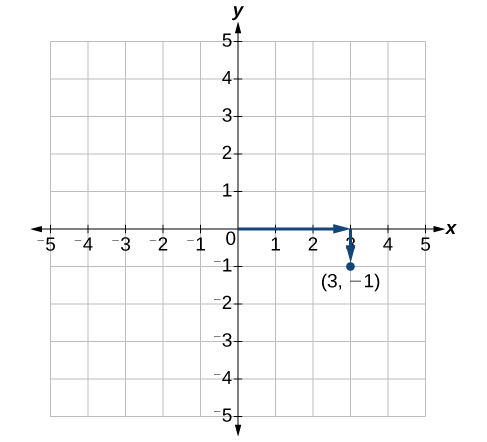
Each point in the plane is identified by its x- coordinate , or horizontal displacement from the origin, and its y- coordinate , or vertical displacement from the origin. Together, we write them as an ordered pair indicating the combined distance from the origin in the form An ordered pair is also known as a coordinate pair because it consists of x- and y -coordinates. For example, we can represent the point in the plane by moving three units to the right of the origin in the horizontal direction, and one unit down in the vertical direction. See [link] .
When dividing the axes into equally spaced increments, note that the x- axis may be considered separately from the y- axis. In other words, while the x- axis may be divided and labeled according to consecutive integers, the y- axis may be divided and labeled by increments of 2, or 10, or 100. In fact, the axes may represent other units, such as years against the balance in a savings account, or quantity against cost, and so on. Consider the rectangular coordinate system primarily as a method for showing the relationship between two quantities.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?