Appendix
Important proofs and derivations
Product Rule
Proof:
Let
and
Write in exponent form.
and
Multiply.
Change of Base Rule
where
and
are positive, and
Proof:
Let
Write in exponent form.
Take the
of both sides.
When
Heron’s Formula
where
Proof:
Let
and
be the sides of a triangle, and
be the height.
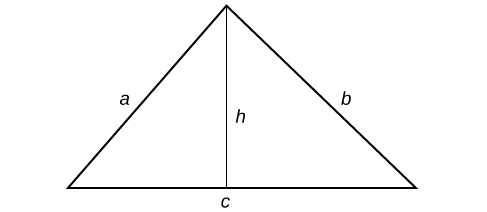
So
.
We can further name the parts of the base in each triangle established by the height such that
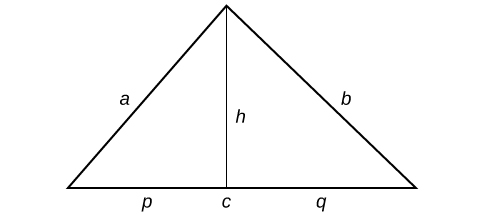
Using the Pythagorean Theorem,
and
Since
then
Expanding, we find that
We can then add
to each side of the equation to get
Substitute this result into the equation
yields
Then replacing
with
gives
Solve for
to get
Since
we get an expression in terms of
and
Therefore,
And since
then
Properties of the Dot Product
Proof:
Proof:
Proof:
Standard Form of the Ellipse centered at the Origin
Derivation
An ellipse consists of all the points for which the sum of distances from two foci is constant:
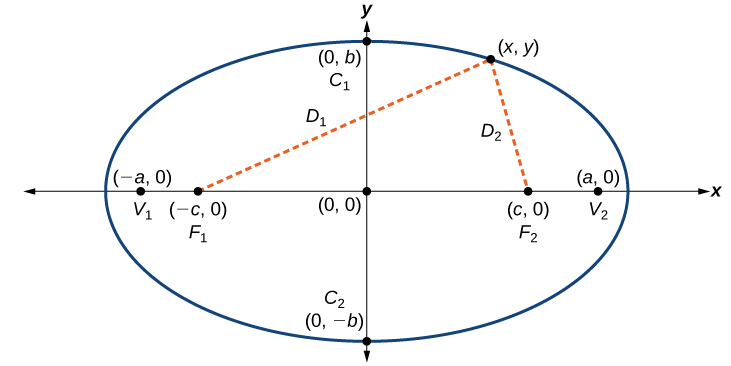
Consider a vertex.
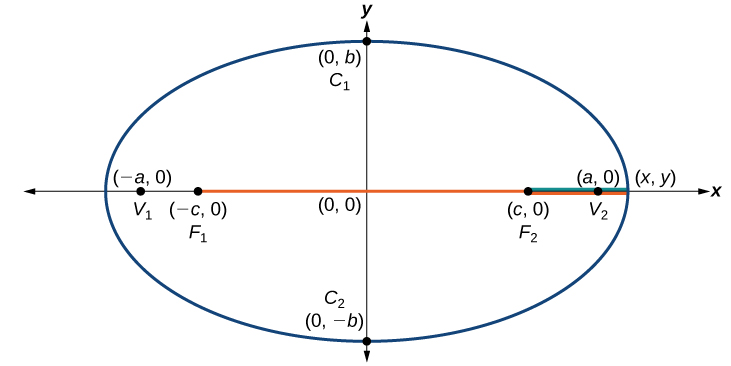
Then,
Consider a covertex.
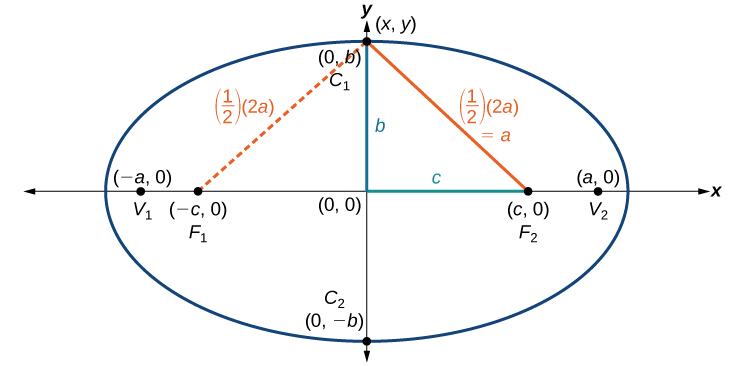
Then
Let
Because
then
Standard Form of the Hyperbola
Derivation
A hyperbola is the set of all points in a plane such that the absolute value of the difference of the distances between two fixed points is constant.
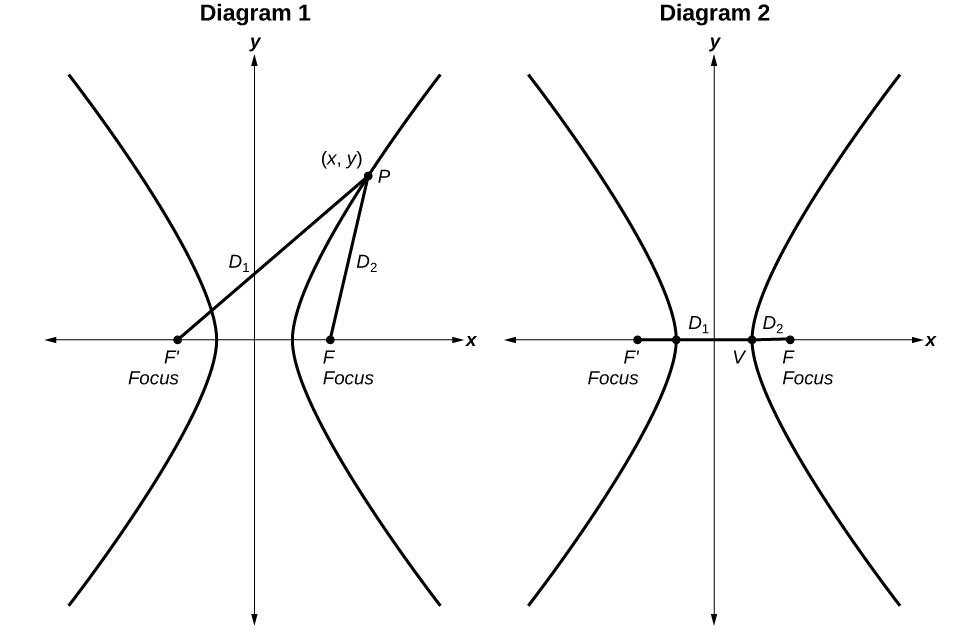
Diagram 1: The difference of the distances from Point
P to the foci is constant:
Diagram 2: When the point is a vertex, the difference is
Define
as a positive number such that
Trigonometric identities
| Pythagorean Identity |
|
| Even-Odd Identities |
|
| Cofunction Identities |
|
| Fundamental Identities |
|
| Sum and Difference Identities |
|
| Double-Angle Formulas |
|
| Half-Angle Formulas |
|
| Reduction Formulas |
|
| Product-to-Sum Formulas |
|
| Sum-to-Product Formulas |
|
| Law of Sines |
|
| Law of Cosines |
|
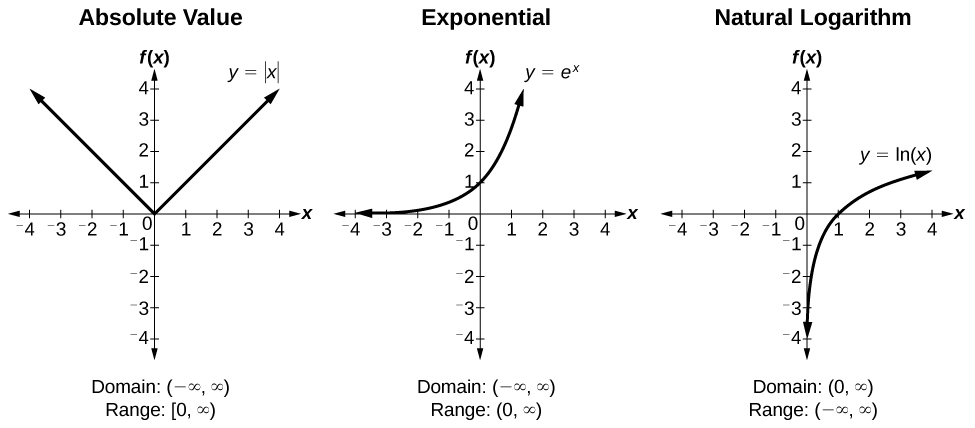
Trigonometric functions
Unit Circle
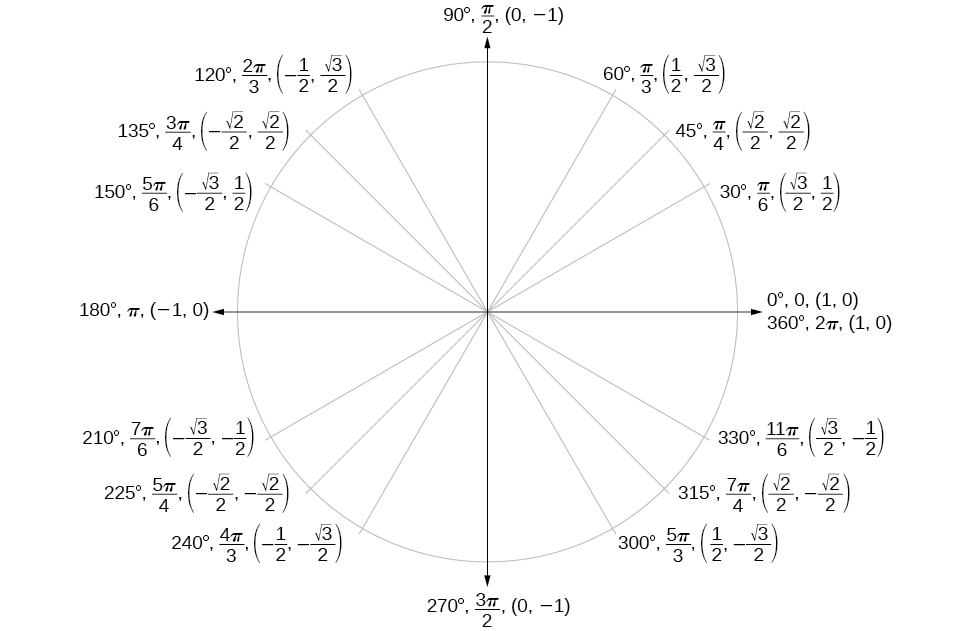
| Angle |
|
|
|
|
|
|
Cosine |
1 |
|
|
|
0 |
|
Sine |
0 |
|
|
|
1 |
|
Tangent |
0 |
|
1 |
|
Undefined |
|
Secant |
1 |
|
|
2 |
Undefined |
|
Cosecant |
Undefined |
2 |
|
|
1 |
|
Cotangent |
Undefined |
|
1 |
|
0 |










