| << Chapter < Page | Chapter >> Page > |
How is the slope of a linear function similar to the derivative?
The slope of a linear function stays the same. The derivative of a general function varies according to Both the slope of a line and the derivative at a point measure the rate of change of the function.
What is the difference between the average rate of change of a function on the interval and the derivative of the function at
A car traveled 110 miles during the time period from 2:00 P.M. to 4:00 P.M. What was the car's average velocity? At exactly 2:30 P.M. , the speed of the car registered exactly 62 miles per hour. What is another name for the speed of the car at 2:30 P.M. ? Why does this speed differ from the average velocity?
Average velocity is 55 miles per hour. The instantaneous velocity at 2:30 p.m. is 62 miles per hour. The instantaneous velocity measures the velocity of the car at an instant of time whereas the average velocity gives the velocity of the car over an interval.
Explain the concept of the slope of a curve at point
Suppose water is flowing into a tank at an average rate of 45 gallons per minute. Translate this statement into the language of mathematics.
The average rate of change of the amount of water in the tank is 45 gallons per minute. If is the function giving the amount of water in the tank at any time then the average rate of change of between and is
For the following exercises, use the definition of derivative to calculate the derivative of each function.
For the following exercises, find the average rate of change between the two points.
For the following polynomial functions, find the derivatives.
For the following functions, find the equation of the tangent line to the curve at the given point on the curve.
For the following exercise, find such that the given line is tangent to the graph of the function.
For the following exercises, consider the graph of the function and determine where the function is continuous/discontinuous and differentiable/not differentiable.
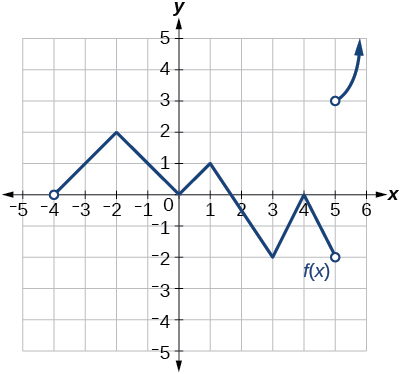
Discontinuous at Not differentiable at -4, –2, 0, 1, 3, 4, 5.
For the following exercises, use [link] to estimate either the function at a given value of or the derivative at a given value of as indicated.
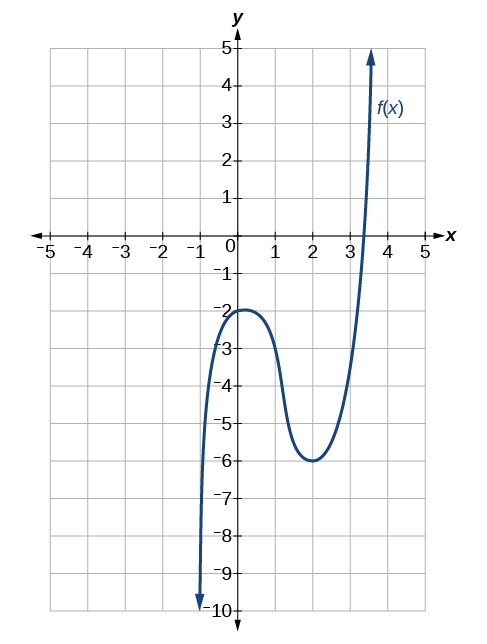
Sketch the function based on the information below:
,
Numerically evaluate the derivative. Explore the behavior of the graph of around by graphing the function on the following domains: , , and . We can use the feature on our calculator that automatically sets Ymin and Ymax to the Xmin and Xmax values we preset. (On some of the commonly used graphing calculators, this feature may be called ZOOM FIT or ZOOM AUTO). By examining the corresponding range values for this viewing window, approximate how the curve changes at that is, approximate the derivative at
Answers vary. The slope of the tangent line near is 2.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?