| << Chapter < Page | Chapter >> Page > |
Describe the altitude of a triangle.
The altitude extends from any vertex to the opposite side or to the line containing the opposite side at a 90° angle.
Compare right triangles and oblique triangles.
When can you use the Law of Sines to find a missing angle?
When the known values are the side opposite the missing angle and another side and its opposite angle.
In the Law of Sines, what is the relationship between the angle in the numerator and the side in the denominator?
What type of triangle results in an ambiguous case?
A triangle with two given sides and a non-included angle.
For the following exercises, assume is opposite side is opposite side and is opposite side Solve each triangle, if possible. Round each answer to the nearest tenth.
For the following exercises, use the Law of Sines to solve for the missing side for each oblique triangle. Round each answer to the nearest hundredth. Assume that angle is opposite side angle is opposite side and angle is opposite side
Find side when
For the following exercises, assume is opposite side is opposite side and is opposite side Determine whether there is no triangle, one triangle, or two triangles. Then solve each triangle, if possible. Round each answer to the nearest tenth.
For the following exercises, use the Law of Sines to solve, if possible, the missing side or angle for each triangle or triangles in the ambiguous case. Round each answer to the nearest tenth.
Find angle when
Find angle when
For the following exercises, find the area of the triangle with the given measurements. Round each answer to the nearest tenth.
For the following exercises, find the length of side Round to the nearest tenth.
For the following exercises, find the measure of angle if possible. Round to the nearest tenth.
For the following exercises, find the area of each triangle. Round each answer to the nearest tenth.
Find the radius of the circle in [link] . Round to the nearest tenth.
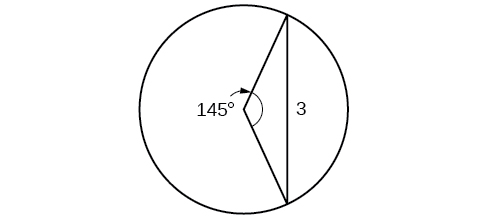
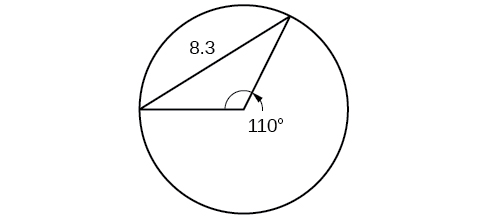
Find the diameter of the circle in [link] . Round to the nearest tenth.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?