| << Chapter < Page | Chapter >> Page > |
At the poles, and , just as is the case without rotation. At any other latitude , the situation is more complicated. The centripetal acceleration is directed toward point P in the figure, and the radius becomes . The vector sum of the weight and must point toward point P , hence no longer points away from the center of Earth. (The difference is small and exaggerated in the figure.) A plumb bob will always point along this deviated direction. All buildings are built aligned along this deviated direction, not along a radius through the center of Earth. For the tallest buildings, this represents a deviation of a few feet at the top.
It is also worth noting that Earth is not a perfect sphere. The interior is partially liquid, and this enhances Earth bulging at the equator due to its rotation. The radius of Earth is about 30 km greater at the equator compared to the poles. It is left as an exercise to compare the strength of gravity at the poles to that at the equator using [link] . The difference is comparable to the difference due to rotation and is in the same direction. Apparently, you really can lose “weight” by moving to the tropics.
Earlier we stated without proof that the law of gravitation applies to spherically symmetrical objects, where the mass of each body acts as if it were at the center of the body. Since [link] is derived from [link] , it is also valid for symmetrical mass distributions, but both equations are valid only for values of . As we saw in [link] , at 400 km above Earth’s surface, where the International Space Station orbits, the value of g is . (We will see later that this is also the centripetal acceleration of the ISS.)
For , [link] and [link] are not valid. However, we can determine g for these cases using a principle that comes from Gauss’s law, which is a powerful mathematical tool that we study in more detail later in the course. A consequence of Gauss’s law, applied to gravitation, is that only the mass within r contributes to the gravitational force. Also, that mass, just as before, can be considered to be located at the center. The gravitational effect of the mass outside r has zero net effect.
Two very interesting special cases occur. For a spherical planet with constant density, the mass within r is the density times the volume within r . This mass can be considered located at the center. Replacing with only the mass within r , , and with r , [link] becomes
The value of g , and hence your weight, decreases linearly as you descend down a hole to the center of the spherical planet. At the center, you are weightless, as the mass of the planet pulls equally in all directions. Actually, Earth’s density is not constant, nor is Earth solid throughout. [link] shows the profile of g if Earth had constant density and the more likely profile based upon estimates of density derived from seismic data.
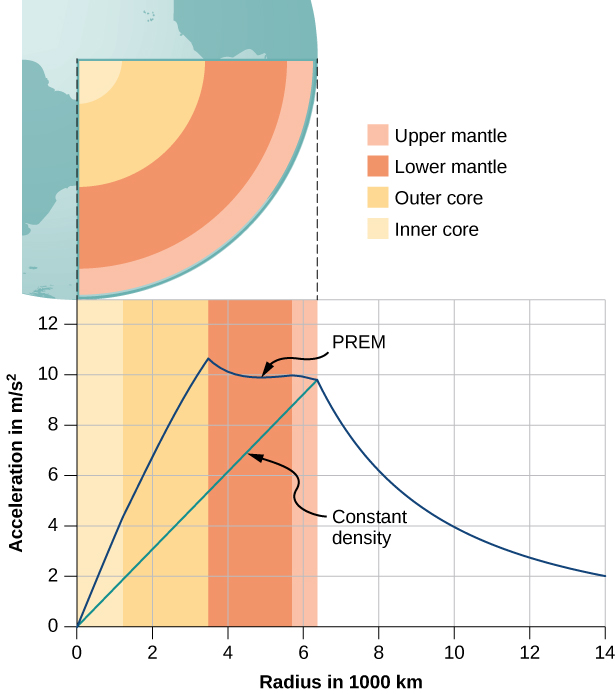
The second interesting case concerns living on a spherical shell planet. This scenario has been proposed in many science fiction stories. Ignoring significant engineering issues, the shell could be constructed with a desired radius and total mass, such that g at the surface is the same as Earth’s. Can you guess what happens once you descend in an elevator to the inside of the shell, where there is no mass between you and the center? What benefits would this provide for traveling great distances from one point on the sphere to another? And finally, what effect would there be if the planet was spinning?
Must engineers take Earth’s rotation into account when constructing very tall buildings at any location other than the equator or very near the poles?
The centripetal acceleration is not directed along the gravitational force and therefore the correct line of the building (i.e., the plumb bob line) is not directed towards the center of Earth. But engineers use either a plumb bob or a transit, both of which respond to both the direction of gravity and acceleration. No special consideration for their location on Earth need be made.
(a) Calculate Earth’s mass given the acceleration due to gravity at the North Pole is measured to be and the radius of the Earth at the pole is 6356 km. (b) Compare this with the NASA’s Earth Fact Sheet value of .
(a) What is the acceleration due to gravity on the surface of the Moon? (b) On the surface of Mars? The mass of Mars is and its radius is .
a. ; b.
(a) Calculate the acceleration due to gravity on the surface of the Sun. (b) By what factor would your weight increase if you could stand on the Sun? (Never mind that you cannot.)
The mass of a particle is 15 kg. (a) What is its weight on Earth? (b) What is its weight on the Moon? (c) What is its mass on the Moon? (d) What is its weight in outer space far from any celestial body? (e) What is its mass at this point?
a. 147 N; b. 25.5 N; c. 15 kg; d. 0; e. 15 kg
On a planet whose radius is , the acceleration due to gravity is . What is the mass of the planet?
The mean diameter of the planet Saturn is , and its mean mass density is . Find the acceleration due to gravity at Saturn’s surface.
The mean diameter of the planet Mercury is , and the acceleration due to gravity at its surface is . Estimate the mass of this planet.
The acceleration due to gravity on the surface of a planet is three times as large as it is on the surface of Earth. The mass density of the planet is known to be twice that of Earth. What is the radius of this planet in terms of Earth’s radius?
A body on the surface of a planet with the same radius as Earth’s weighs 10 times more than it does on Earth. What is the mass of this planet in terms of Earth’s mass?

Notification Switch
Would you like to follow the 'University physics volume 1' conversation and receive update notifications?