| << Chapter < Page | Chapter >> Page > |
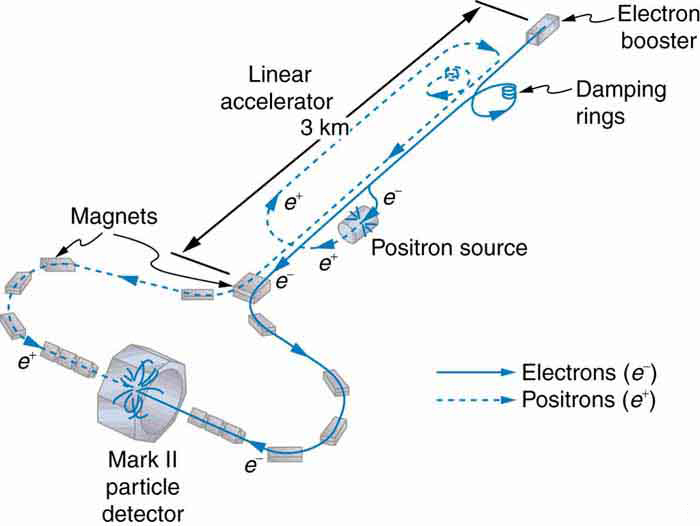
In addition to the large synchrotrons that produce colliding beams of protons and antiprotons, there are other large electron-positron accelerators. The oldest of these was a straight-line or linear accelerator , called the Stanford Linear Accelerator (SLAC), which accelerated particles up to 50 GeV as seen in [link] . Positrons created by the accelerator were brought to the same energy and collided with electrons in specially designed detectors. Linear accelerators use accelerating tubes similar to those in synchrotrons, but aligned in a straight line. This helps eliminate synchrotron radiation losses, which are particularly severe for electrons made to follow curved paths. CERN had an electron-positron collider appropriately called the Large Electron-Positron Collider (LEP), which accelerated particles to 100 GeV and created a collision energy of 200 GeV. It was 8.5 km in diameter, while the SLAC machine was 3.2 km long.
A linear accelerator designed to produce a beam of 800-MeV protons has 2000 accelerating tubes. What average voltage must be applied between tubes (such as in the gaps in [link] ) to achieve the desired energy?
Strategy
The energy given to the proton in each gap between tubes is where is the proton’s charge and is the potential difference (voltage) across the gap. Since and , the proton gains 1 eV in energy for each volt across the gap that it passes through. The AC voltage applied to the tubes is timed so that it adds to the energy in each gap. The effective voltage is the sum of the gap voltages and equals 800 MV to give each proton an energy of 800 MeV.
Solution
There are 2000 gaps and the sum of the voltages across them is 800 MV; thus,
Discussion
A voltage of this magnitude is not difficult to achieve in a vacuum. Much larger gap voltages would be required for higher energy, such as those at the 50-GeV SLAC facility. Synchrotrons are aided by the circular path of the accelerated particles, which can orbit many times, effectively multiplying the number of accelerations by the number of orbits. This makes it possible to reach energies greater than 1 TeV.
The total energy in the beam of an accelerator is far greater than the energy of the individual beam particles. Why isn’t this total energy available to create a single extremely massive particle?
Synchrotron radiation takes energy from an accelerator beam and is related to acceleration. Why would you expect the problem to be more severe for electron accelerators than proton accelerators?
What two major limitations prevent us from building high-energy accelerators that are physically small?
What are the advantages of colliding-beam accelerators? What are the disadvantages?
At full energy, protons in the 2.00-km-diameter Fermilab synchrotron travel at nearly the speed of light, since their energy is about 1000 times their rest mass energy.
(a) How long does it take for a proton to complete one trip around?
(b) How many times per second will it pass through the target area?
(a)
(b)
Suppose a created in a bubble chamber lives for What distance does it move in this time if it is traveling at 0.900 c ? Since this distance is too short to make a track, the presence of the must be inferred from its decay products. Note that the time is longer than the given lifetime, which can be due to the statistical nature of decay or time dilation.
What length track does a traveling at 0.100 c leave in a bubble chamber if it is created there and lives for ? (Those moving faster or living longer may escape the detector before decaying.)
78.0 cm
The 3.20-km-long SLAC produces a beam of 50.0-GeV electrons. If there are 15,000 accelerating tubes, what average voltage must be across the gaps between them to achieve this energy?
Because of energy loss due to synchrotron radiation in the LHC at CERN, only 5.00 MeV is added to the energy of each proton during each revolution around the main ring. How many revolutions are needed to produce 7.00-TeV (7000 GeV) protons, if they are injected with an initial energy of 8.00 GeV?
A proton and an antiproton collide head-on, with each having a kinetic energy of 7.00 TeV (such as in the LHC at CERN). How much collision energy is available, taking into account the annihilation of the two masses? (Note that this is not significantly greater than the extremely relativistic kinetic energy.)
When an electron and positron collide at the SLAC facility, they each have 50.0 GeV kinetic energies. What is the total collision energy available, taking into account the annihilation energy? Note that the annihilation energy is insignificant, because the electrons are highly relativistic.
100 GeV

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?