| << Chapter < Page | Chapter >> Page > |
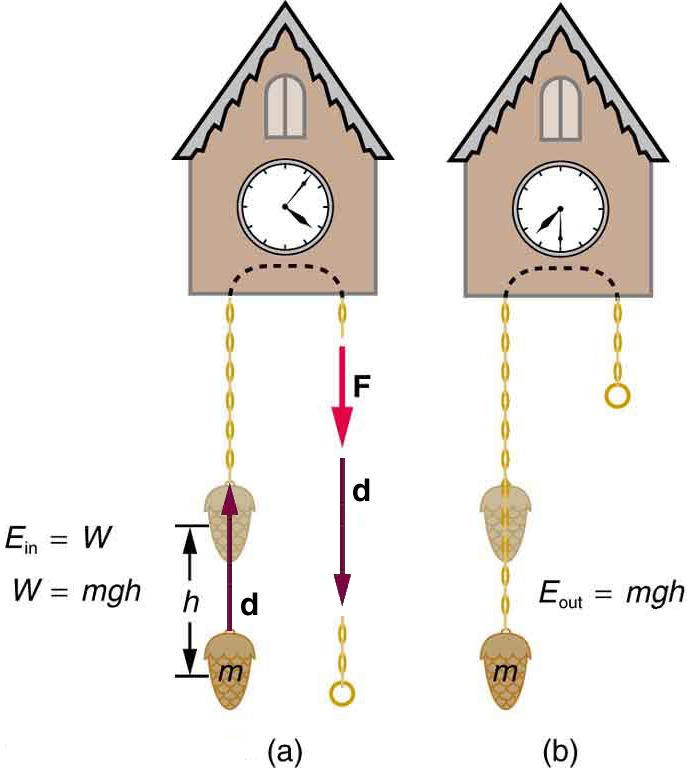
Gravitational potential energy may be converted to other forms of energy, such as kinetic energy. If we release the mass, gravitational force will do an amount of work equal to on it, thereby increasing its kinetic energy by that same amount (by the work-energy theorem). We will find it more useful to consider just the conversion of to without explicitly considering the intermediate step of work. (See [link] .) This shortcut makes it is easier to solve problems using energy (if possible) rather than explicitly using forces.
More precisely, we define the change in gravitational potential energy to be
where, for simplicity, we denote the change in height by rather than the usual . Note that is positive when the final height is greater than the initial height, and vice versa. For example, if a 0.500-kg mass hung from a cuckoo clock is raised 1.00 m, then its change in gravitational potential energy is
Note that the units of gravitational potential energy turn out to be joules, the same as for work and other forms of energy. As the clock runs, the mass is lowered. We can think of the mass as gradually giving up its 4.90 J of gravitational potential energy, without directly considering the force of gravity that does the work .
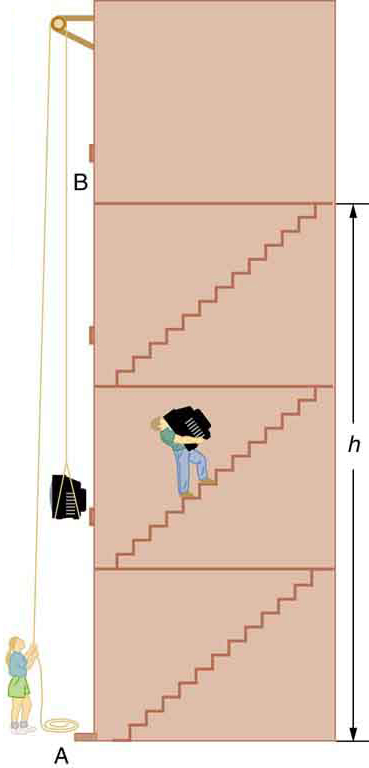
The equation applies for any path that has a change in height of , not just when the mass is lifted straight up. (See [link] .) It is much easier to calculate (a simple multiplication) than it is to calculate the work done along a complicated path. The idea of gravitational potential energy has the double advantage that it is very broadly applicable and it makes calculations easier. From now on, we will consider that any change in vertical position of a mass is accompanied by a change in gravitational potential energy , and we will avoid the equivalent but more difficult task of calculating work done by or against the gravitational force.
A 60.0-kg person jumps onto the floor from a height of 3.00 m. If he lands stiffly (with his knee joints compressing by 0.500 cm), calculate the force on the knee joints.
Strategy
This person’s energy is brought to zero in this situation by the work done on him by the floor as he stops. The initial is transformed into as he falls. The work done by the floor reduces this kinetic energy to zero.
Solution
The work done on the person by the floor as he stops is given by
with a minus sign because the displacement while stopping and the force from floor are in opposite directions . The floor removes energy from the system, so it does negative work.
The kinetic energy the person has upon reaching the floor is the amount of potential energy lost by falling through height :
The distance that the person’s knees bend is much smaller than the height of the fall, so the additional change in gravitational potential energy during the knee bend is ignored.
The work done by the floor on the person stops the person and brings the person’s kinetic energy to zero:
Combining this equation with the expression for gives
Recalling that is negative because the person fell down , the force on the knee joints is given by
Discussion
Such a large force (500 times more than the person’s weight) over the short impact time is enough to break bones. A much better way to cushion the shock is by bending the legs or rolling on the ground, increasing the time over which the force acts. A bending motion of 0.5 m this way yields a force 100 times smaller than in the example. A kangaroo's hopping shows this method in action. The kangaroo is the only large animal to use hopping for locomotion, but the shock in hopping is cushioned by the bending of its hind legs in each jump.(See [link] .)

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?