| << Chapter < Page | Chapter >> Page > |
By the end of this section, you will be able to:

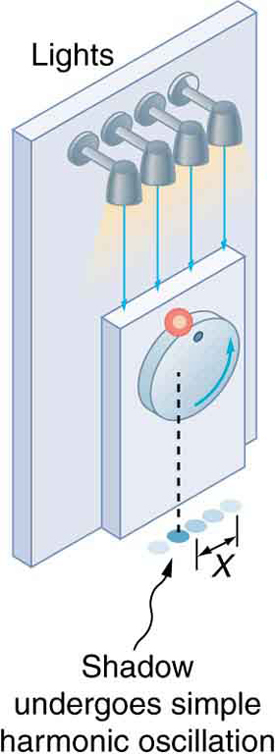
There is an easy way to produce simple harmonic motion by using uniform circular motion. [link] shows one way of using this method. A ball is attached to a uniformly rotating vertical turntable, and its shadow is projected on the floor as shown. The shadow undergoes simple harmonic motion. Hooke’s law usually describes uniform circular motions ( constant) rather than systems that have large visible displacements. So observing the projection of uniform circular motion, as in [link] , is often easier than observing a precise large-scale simple harmonic oscillator. If studied in sufficient depth, simple harmonic motion produced in this manner can give considerable insight into many aspects of oscillations and waves and is very useful mathematically. In our brief treatment, we shall indicate some of the major features of this relationship and how they might be useful.
[link] shows the basic relationship between uniform circular motion and simple harmonic motion. The point P travels around the circle at constant angular velocity . The point P is analogous to an object on the merry-go-round. The projection of the position of P onto a fixed axis undergoes simple harmonic motion and is analogous to the shadow of the object. At the time shown in the figure, the projection has position and moves to the left with velocity . The velocity of the point P around the circle equals .The projection of on the -axis is the velocity of the simple harmonic motion along the -axis.
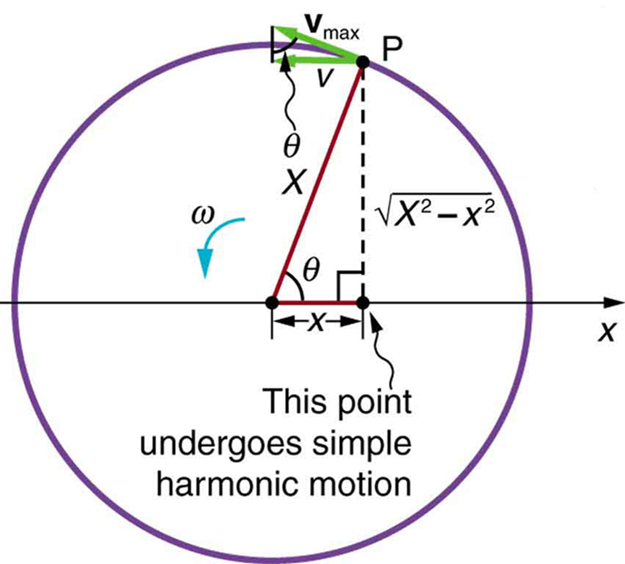
To see that the projection undergoes simple harmonic motion, note that its position is given by
where , is the constant angular velocity, and is the radius of the circular path. Thus,
The angular velocity is in radians per unit time; in this case radians is the time for one revolution . That is, . Substituting this expression for , we see that the position is given by:
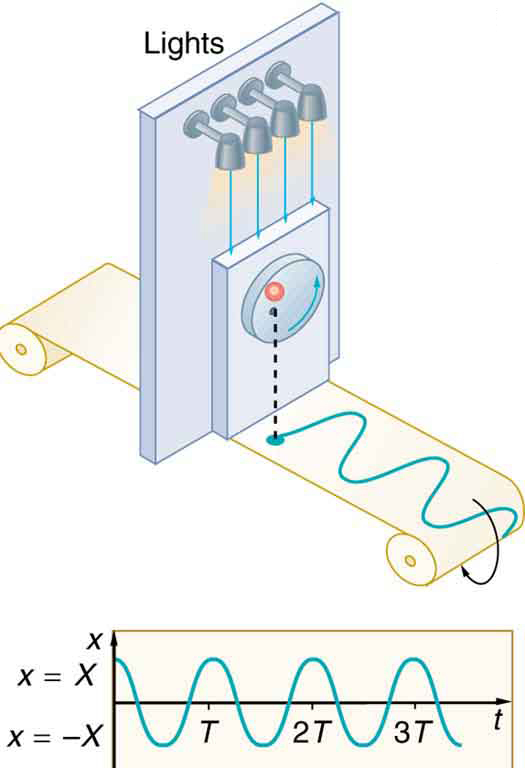
This expression is the same one we had for the position of a simple harmonic oscillator in Simple Harmonic Motion: A Special Periodic Motion . If we make a graph of position versus time as in [link] , we see again the wavelike character (typical of simple harmonic motion) of the projection of uniform circular motion onto the -axis.

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?