3.21 Sspd_chapter 1_part 9_conclusion_removal of degeneracy  (Page 4/4)

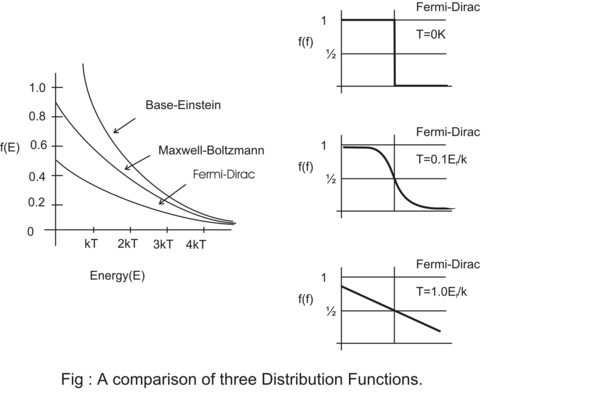
Fig(1.36) A comparison of three Distribution Functions.

1.8.2.3. COMPARISON BETWEEN BOSE-EINSTEIN AND FERMI-DIRAC DISTRIBUTION.

When indistinguishable particles like photons are brought together they create attraction and there is a tendency of clustering. In an elemental phase space many photons can be accommodated at the same energy state at the same time and there will be no opposition to this tendency of clustering.

But if distinguishable particle like electrons are brought in an elemental phase space then at most two electrons of opposite spin ±(1/2)ћ can be accommodated and all other electrons will be repelled. This is called degeneracy pressure.

When a Main Sequence star runs out of its fusion fuel , generation of fusion energy stops and gravitational collapse restarts leading to the formation of White dwarf. The gravitational collapse is finally checked by the degeneracy pressure developed by tightly packed electrons. This is due to the fact that electrons are fermions and not more than two electrons can be accommodated in an elemental phase space.

The phase space has three spatial axes (x, y, z) and three momentum axes (p _x , p _y , p _z ).

An elemental phase space = ΔV= Δx. Δy. Δz. Δp _x . Δp _y .Δp _z

But Δx. Δp _x >ћ,

Δy. Δp _y >ћ,

Δz. Δp _z >ћ, from Heisenberg Uncertainty Principle.

Therefore ΔV ≥ ћ ³ ,

Every elemental phase space has a spatial coordinate x _n , y _n , z _n and momentum coordinates are p _{xn ,} p _yn .p _zn .

In circuit theory we have studied Laplace Transform and in Signal Processing we have studied Fourier Transform. In both cases we have studied the Time Domain Representation and Frequency Domain Representation of the signals.

In an exactly identical manner we have a transformation from Real Space to Phase Space in case of Atomic electrons

In Real Space, the orbiting electrons have sets of four quantum numbers (n, l, m, s).

In Phase Space, every elemental phase space is filled with opposite spin electrons. With every elemental phase space , we have a set of four quantum numbers associated (n) _N , (l) _N (m) _N (±1/2) _N . Therefore no two sets of quantum numbers are identical This gives rise to Pauli’s Exclusion Principle which states that no two electrons can have all the four quantum numbers identical. In a given phase space, the two opposite spin electrons have identical n , l. m but opposite spin . Thus no two electrons are ever identical in all four quantum numbers.

Sec(1.8.1) indicates that electrons have 2n ² -fold degeneracy in nth Shell. As we saw this was incorrect because we had taken non-relativistic Hamiltonian. If relativistic Hamiltonian is considered then we have:

E= -13.6eV/(n+l+1) 2 1.81

. Through this equation n-fold degeneracy is removed by taking into account the eccentricity of the ellipsoidal subshell in which the electrons of a given “l” are placed. Thus partial removal of degeneracy is accounted for as shown in Fig(1.37).

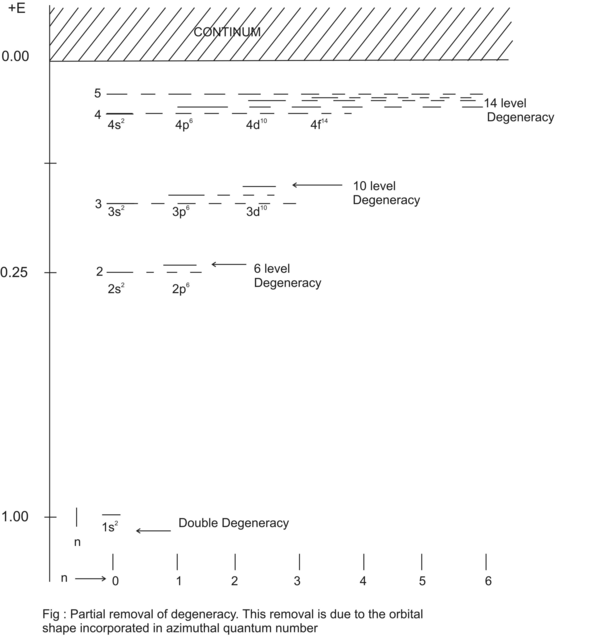
Figure 1.37. Partial temoval of degeneracy. This removal is due to the orbital shape incorporated in azimuthial quantum number.

When n=3 then l=0 (perfectly spherical orbit), 1(ellipsoidal orbit), 2(elongated orbit). These three azimuthial numbers cause the degenerate levels to split apart. Thus three fold degeneracy is removed.

When the atom is put in a magnetic field then remaining 6 fold degeneracy is removed. This is due to the magnetic moment caused due to orbital angular momentum and spin angular momentum. Magnetic moment is vector quantity. Hence it is positive when aligned with the Magnetic field and negative when it is anti-parallel.Let us consider the sub shell n=3 and l =2. In this subshell each electron has orbital angular momentum of L _Z =ћ√6.

Projections of the orbital angular momentum on the magnetic field are 2ћ, 1 ћ,

0 ћ, -1 ћ, -2 ћ. Magnetic interaction will remove five-fold degeneracy.

Total spin angular momentum is ћ√((1/2)(3/2)). This has two projections

There are 10 electrons in this sub shell (n=3, l=2) : 2(opposite spins) at m= -2 , 2(opposite spins) at m= -1, 2(opposite spins) at m= 0, 2(opposite spins) at m=1, 2(opposite spins) at m=2.. When a magnetic field is applied these 10 electrons interact with the applied magnetic field to split in 10 discrete levels.

The z-axis projection of L and S give a total projection of J _Z =L _Z + S _Z .

Hence the 10 electrons produce a projection of:

(2±1/2)ћ , (1±1/2)ћ, (0±1/2)ћ, (-1±1/2)ћ, (-2±1/2)ћ on the z-axis. Thus we have 10 discrete and separate magnetic moments resulting into 10 discrete and separate energy levels as a result of the interaction among the applied magnetic field and the magnetic moments. Thus total degeneracy, as shown in Fig(1.35), is removed with the application of the magnetic field. It is because of the removal of degeneracy that we see many more closely spaced lines in the line spectra of an elemental gas than that expected from Bohr’s model.

Stern-Gerlach experiment shown in Figure(1.38) demonstrates the effect of an applied magnetic field upon non-polarized atomic beam.

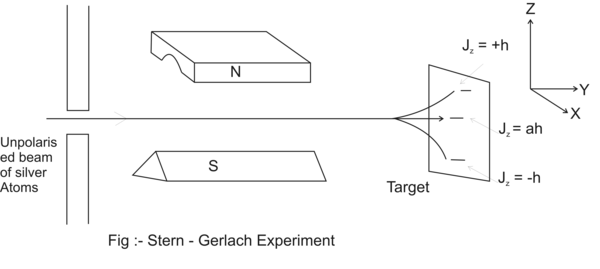
Figure(1.38) Stern-Gerlach Experiment.

As shown in the Fig (1.38) an unpolarized atom beam passes through a highly non-uniform magnetic field.

Magnetic field is directed in Z direction. The atoms have a net angular momentum of ћ√2 = J.

These angular momenta have three possible projections on Z axis:

J _z1 = +ћ

J _z0 = 0ћ

J _z-1 = -ћ

The three projections have three magnetic moments.

Magnetic Moments are: μ _z = gJ _z = +g ћ = μ ₊₁

0 = μ ₀

-g ћ = μ _-1

The non-uniform magnetic field creates a magnetic field gradient which interacts with three different kinds of magnetic moments to create 3 different beams of atoms. The scattering forces, which split the beam, are:

F ₊₁ = (μ ₊₁ )[∂H/∂z]

F ₀ = 0

F _-1 = (μ _-1 )[∂H/∂z]

F ₊₁ causes a portion of beam to be bent in positive Z direction.

F _-1 causes another portion of beam to be bent in negative Z direction.

F ₀ causes no beam bending.

Thus magnetic field interaction causes the un-polarized beam to split in three distinct portions hitting the target at three separate zones. This establishes that magnetic quantum number is associated with electrons.

1.8.3. BRIEF REVIEW OF THE QUANTUM NATURE OF BOUNDED ELECTRONS.

In this chapter we have established that

1. the bounded electrons have four quantum numbers namely n, l, m and s;
2. for any two electrons all the four quantum numbers can never be identical;

The first proposition establishes the electrons as distinguishable particles. Because they are distinguishable, they follow Fermi-Dirac Statistics. This results in anti-symmetric wave function for electrons which compels electrons to follow Pauli –Exclusion Principle.