3.13 Sspd_chapter1_part 8_electron in a potential well_formulation  (Page 2/2)

In contrast sound wave is a longitudinal wave because the medium particles oscillate in the same direction as the direction of propagation.

In an identical manner Schrodinger [Appendix XXXV] proposed the progressive matter wave:

In 1926 Schrodinger stated the Hamiltonian Equation:

H. ψ = E. ψ

where H is the Hamiltonian [Appendix XXXVI ] Energy Operator =p ² /(2m) + V(r);

and E is the total energy;

Using this Schrodinger Equation, solutions are obtained for an electron in a Hydrogen atom and the four quantum numbers are predicted namely Principal Quantum Number(n), Azimuthial Quantum Number (l), Magnetic Quantum Number (m) and Spin Quantum Number (s). These quantum numbers correctly explain the experimental results.

Still there was no direct proof for the existence of matter wave.

The mathematical form of the solution of Schrodinger Equation is :

ψ(z,t) = ψ 0 .Exp[j(k z .z - ω.t)] 1.42

Where k _z = 2π/λ _z = wave propogation vector or wave number;

And ω = 2 π ν = circular frequency;

And ψ = probability amplitude;

And ψ .ψ* = | ψ | ² = probability density = probability of finding the particle per unit volume;

| ψ | ² dV= probability of finding the particle in an elemental volume.

If | ψ | ² dV is integrated over the total volume where the particle is likely to be found then the integral will come out to be unity. This means the particle is certainly present in the given volume over which the integration has been carried out.

If the integral is zero then it means it is impossible to find the particle in the given volume.

If integral is between 0 and 1 say 0.5 that means if hundred observations are made within the given volume then in fifty observations the particle is likely to be detected.

If integral is 0.25 then it implies that out of 100 observations 25 times the particle will be observed.

Therefore closed ∫ _V [| ψ | ² dV] = probability of finding the particle in volume V;

Therefore ∫ V [| ψ | 2 dV] = 1 implies certainty of finding the particle in V 1.43

And ∫ V [| ψ | 2 dV]<1 implies less than 100% probability of finding the particle in volume V 1.44

In spite of this correctness there were no direct experimental proofs for the matter wave though a THOUGHT EXPERIMENT had been proposed in early 70’s.

In 1985 this thought experiment was practically performed as shown in Figure(1.22).

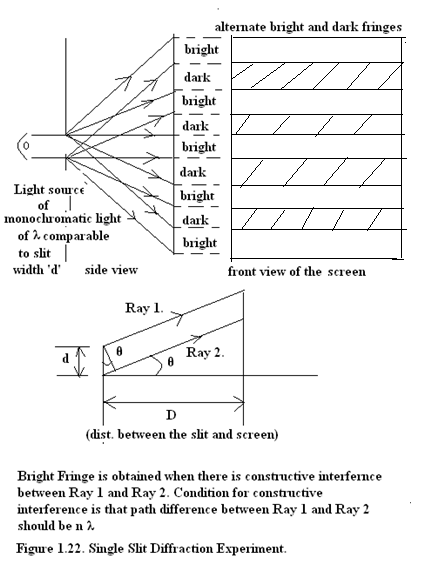
Fig(1.22) Single slit light diffraction experiment.

Path length of ray 1 is = D/CosӨ

Path length of ray 2 is = D/CosӨ + d.SinӨ

Therefore the path difference = d.SinӨ

When d.SinӨ = nλ then we have a bright fringe and

When d.SinӨ = (n+ ½)λ then we obtain a dark fringe. Thus Single Slit Diffractin pattern of light consists of alternate bright and dark fringes.

If instead of light we use a very weak source of electrons then instead of bright and dark fringes we obtain the high and low probability of finding the electrons on different parts of the screen.

For this experiment the electron source should be weak enough to pass singally or one by one through the single slit. As a detector the positively charged anode plate should be used and the whole diffraction set up should be installed in an evacuated chamber as shown in Fig(1.23). The strength of current picked up from different parts of the screen is directly proportional to the probability of incidence of the incident electrons. In place of bright fringe we will obtain a large current and in place of dark fringe we will obtain a small current.

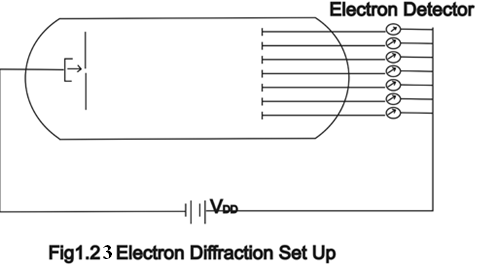
Fig(1.23) Electron Diffraction Set Up.

After giving a physical interpretation of the matter wave we will come to the statement of Schrodinger Equation.

Position (z) and momentum in z direction (p _z ) are defined as canonical conjugate variables.

Similarly time (t) and energy (E) are also defined as canonical conjugate variables.

Momentum p _z is defined as operator iћ∂/∂z and

Energy E is defined as -iћ∂/∂t .

Schrodinger used

Hamiltonian Operaror H = Kinetic Energy Operator + Potential Energy Operator.

Therefore H = p 2 /(2m) + V(z) 1.45

When Operator H operates upon a matter wave then it yields the Eigen value of the energy of the matter wave.

Therefore Hψ = Eψ 1.46

Therefore [p ² /(2m) + V(z)] ψ = Eψ

Substituting p operator we get:

[-(ћ ² /2m) ∂ ² /∂x ² + V(z)]ψ = Eψ

Therefore -(ћ ² /2m) ∂ ² ψ /∂z ² = [E-V(x)] ψ

Or (ћ 2 /2m) ∂ 2 ψ /∂z 2 + [E-V(z)] ψ = 0 1.47

This is a second order linear differential equation known as the Schrodinger Equation and this has a standard procedure for its solution.