| << Chapter < Page | Chapter >> Page > |
Basisoppervlakte = s 2 = 28 2 = 784 mm 2
Stap 3: Bereken die basisomtrek.
Basisomtrek = 4 × s = 112mm
Stap 4: Skryf die prismahoogte neer
H = 52mm
Stap 5: Bereken die TBO en V.
V = 784 × 52 = 40 768 mm 3 ≈ 40,7 cm 3
TBO = (2 × 784) + (52 × 112) = 7 392 mm 2 ≈ 73,9 cm 2

1 = 41mm; b = 14mm
Stap 1: Bepaal waar die basis is en skets dit saam met die afmetings.
Stap 2: Bereken die basisoppervlakte.
Basisoppervlakte = l × b = 41 × 14 = 574 mm 2
Stap 3: Bereken die basisomtrek.
Basisomtrek = 2 (14 + 41) = 110mm
Stap 4: Skryf die prismahoogte neer
H = 54mm
Stap 5: Bereken die TBO en V.
V = 574 × 54 = 30 996 mm 3 ≈ 31 cm 3
TBO = (2 × 574) + (54 × 110) = 7 088 mm 2 ≈ 70,1 cm 2
TBO = 2 basisoppervlakte + sy-oppervlakte = 2 (π r 2 ) + (H × basisomtrek)

r = 17,5mm
Stap 1: Bepaal waar die basis is en skets dit saam met die afmetings.
Stap 2: Bereken die basisoppervlakte.
Basisoppervlakte = π r 2 = 3,14159 × (17,5) 2 ≈ 962,1mm 2
Stap 3: Bereken die basisomtrek.
Basisomtrek = 2 π r = 109,956mm
Stap 4: Skryf die prismahoogte neer
H = 60,5mm
Stap 5: Bereken die TBO en V.
V = 962,1 × 60,5 ≈ 58 207,8 mm 3 ≈ 58 cm 3
TBO = (2 × 962,1) + (60.5 × 109,956) ≈ 8 576,55 mm 2 ≈ 85,8 cm 2
TBO = 2 basisoppervlakte + sy-oppervlakte = 2 (½ × b × h) + (H × basisomtrek)
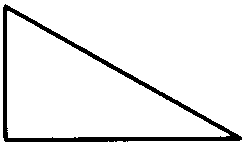
b = 43,5mm; h = 31,5mm skuinssy = 53,7mm (Pyth.)
Stap 1: Bepaal waar die basis is en skets dit saam met die afmetings.
Stap 2: Bereken die basisoppervlakte.
Basisoppervlakte = ½ b × h = 685,125 ≈ 685,1mm 2
Stap 3: Bereken die basisomtrek.
Basisomtrek = b + h + skuinssy ≈ 128,7mm
Stap 4: Skryf die prismahoogte neer
H = 60,5mm
Stap 5: Bereken die TBO en V.
V = 685,1 × 60,5 ≈ 41 450,1 mm 3 ≈ 41 cm 3
TBO = (2 × 685,1) + (60.5 × 128,7) ≈ 9 157,06 mm 2 ≈ 91,6 cm 2
Oefening:
Bereken die totale buite-oppervlakte en die volume van die volgende drie prismas.
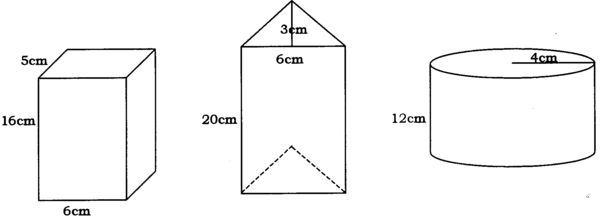
Opdrag om in pare te doen:
Aktiwiteit 2
Om vertroud te raak met verskeie twee- en driedimensionele figure
[LU 3.1, 3.5]
A. Tweedimensionele figure
Dit is figure wat op ‘n vel papier geteken kan word. Hulle is dus plat figure. Daar is natuurlik ontelbaar baie sulke figure.
Veelhoeke (poligone) is geslote figure met drie of meer reguit sye. As al die sye ewe lank is en al die binnehoeke ewe groot, praat ons van reëlmatige veelhoeke. Driehoeke is driesydige veelhoeke, en ‘n gelyksydige driehoek is ‘n reëlmatige driesydige veelhoek. ‘n Vierkant is ‘n reëlmatige viersydige veelhoek. Penta gone (vyfhoeke) het vyf sye, heksagone het ses sye en heptagone het sewe. Maak ‘n lys van al hierdie spesiale name wat jy kan opspoor.

Notification Switch
Would you like to follow the 'Wiskunde graad 9' conversation and receive update notifications?