| << Chapter < Page | Chapter >> Page > |
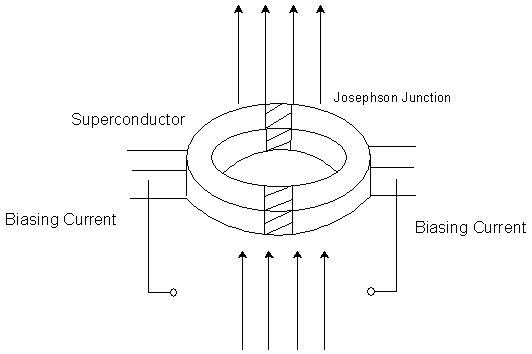
Josephson predicted that a superconducting current can be sustained in the loop, even if its path is interrupted by an insulating barrier or a normal metal. The SQUID has two such barriers or ‘Josephson junctions’. Both junctions introduce the same phase difference when the magnetic flux through the loop is 0, Φ 0 , 2 Φ 0 and so on, which results in constructive interference, and they introduce opposite phase difference when the flux is Φ 0 /2, 3 Φ 0 /2 and so on, which leads to destructive interference. This interference causes the critical current density, which is the maximum current that the device can carry without dissipation, to vary. The critical current is so sensitive to the magnetic flux through the superconducting loop that even tiny magnetic moments can be measured. The critical current is usually obtained by measuring the voltage drop across the junction as a function of the total current through the device. Commercial SQUIDs transform the modulation in the critical current to a voltage modulation, which is much easier to measure.
An applied magnetic field produces a phase change around a ring, which in this case is equal
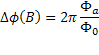
where Φ a is the flux produced in the ring by the applied magnetic field. The magnitude of the critical measuring current is dependent upon the critical current of the weak-links and the limit of the phase change around the ring being an integral multiple of 2 π . For the whole ring to be superconducting the following condition must be met
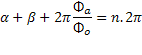
where α and β are the phase changes produced by currents across the weak-links and 2πΦ a /Φ o is the phase change due to the applied magnetic field.
When the measuring current is applied α and β are no longer equal, although their sum must remain constant. The phase changes can be written as
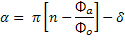
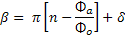
where δ is related to the measuring current I. Using the relation between current and phase from the above Eqn. and rearranging to eliminate i we obtain an expression for I,
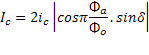
As sinδ cannot be greater than unity we can obtain the critical measuring current, I c from the above
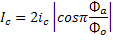
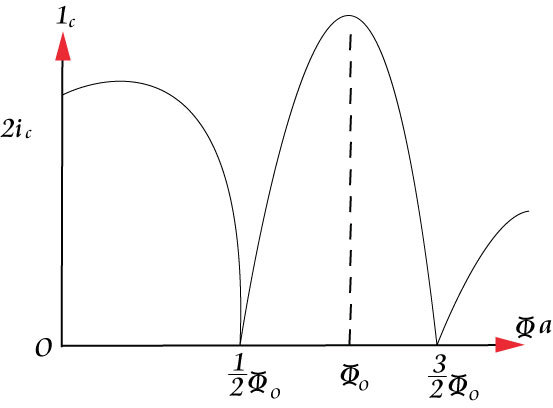
which gives a periodic dependence on the magnitude of the magnetic field, with a maximum when this field is an integer number of fluxons and a minimum at half integer values as shown in the below figure.

Notification Switch
Would you like to follow the 'Nanomaterials and nanotechnology' conversation and receive update notifications?