| << Chapter < Page | Chapter >> Page > |
These arguments about the shapes of indifference curves and about higher or lower levels of utility do not require any numerical estimates of utility, either by the individual or by anyone else. They are only based on the assumptions that when people have less of one good they need more of another good to make up for it, if they are keeping the same level of utility, and that as people have more of a good, the marginal utility they receive from additional units of that good will diminish. Given these gentle assumptions, a field of indifference curves can be mapped out to describe the preferences of any individual.
The Individuality of Indifference Curves
Each person determines their own preferences and utility. Thus, while indifference curves have the same general shape—they slope down, and the slope is steeper on the left and flatter on the right—the specific shape of indifference curves can be different for every person. [link] , for example, applies only to Lilly’s preferences. Indifference curves for other people would probably travel through different points.
People seek the highest level of utility, which means that they wish to be on the highest possible indifference curve. However, people are limited by their budget constraints, which show what tradeoffs are actually possible.
Maximizing Utility at the Highest Indifference Curve
Return to the situation of Lilly’s choice between paperback books and doughnuts. Say that books cost $6, doughnuts are 50 cents each, and that Lilly has $60 to spend. This information provides the basis for the budget line shown in [link] . Along with the budget line are shown the three indifference curves from [link] . What is Lilly’s utility-maximizing choice? Several possibilities are identified in the diagram.
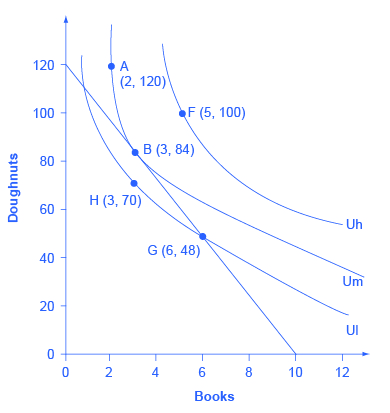
The choice of F with five books and 100 doughnuts is highly desirable, since it is on the highest indifference curve Uh of those shown in the diagram. However, it is not affordable given Lilly’s budget constraint. The choice of H with three books and 70 doughnuts on indifference curve Ul is a wasteful choice, since it is inside Lilly’s budget set, and as a utility-maximizer, Lilly will always prefer a choice on the budget constraint itself. Choices B and G are both on the opportunity set. However, choice G of six books and 48 doughnuts is on lower indifference curve Ul than choice B of three books and 84 doughnuts, which is on the indifference curve Um. If Lilly were to start at choice G, and then thought about whether the marginal utility she was deriving from doughnuts and books, she would decide that some additional doughnuts and fewer books would make her happier—which would cause her to move toward her preferred choice B. Given the combination of Lilly’s personal preferences, as identified by her indifference curves, and Lilly’s opportunity set, which is determined by prices and income, B will be her utility-maximizing choice.

Notification Switch
Would you like to follow the 'Principles of economics' conversation and receive update notifications?