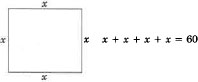This module is from Elementary Algebra by Denny Burzynski and Wade Ellis, Jr.
In this chapter, the emphasis is on the mechanics of equation solving, which clearly explains how to isolate a variable. The goal is to help the student feel more comfortable with solving applied problems. Ample opportunity is provided for the student to practice translating words to symbols, which is an important part of the "Five-Step Method" of solving applied problems (discussed in modules (<link document="m21980"/>) and (<link document="m21979"/>)).
Objectives of this module: be able to solve various applied problems.
Overview
Solving applied problems
Let’s study some interesting problems that involve linear equations in one variable. In order to solve such problems, we apply the following five-step method:
Five-step method for solving word problems
- Let
(or some other letter) represent the unknown quantity.
- Translate the words to mathematical symbols and form an equation.
- Solve this equation.
- Ask yourself "Does this result seem reasonable?" Check the solution by substituting the result into the original statement of the problem.
If the answer doesn’t check, you have either solved the equation incorrectly, or you have developed the wrong equation. Check your method of solution first. If the result does not check, reconsider your equation.
- Write the conclusion.
If it has been your experience that word problems are difficult, then follow the five-step method carefully. Most people have difficulty because they neglect step 1.
Always start by INTRODUCING A VARIABLE!
Keep in mind what the variable is representing throughout the problem.
Sample set a
This year an item costs
, an increase of
over last year’s price. What was last year’s price?
Got questions? Get instant answers now!
Practice set a
This year an item costs
, an increase of
over last year’s price. What was last year’s price?
- Let
- Last year's price was
.
Last year's price was
Got questions? Get instant answers now!
Sample set b
The perimeter (length around) of a square is 60 cm (centimeters). Find the length of a side.
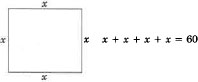
Got questions? Get instant answers now!
Practice set b
The perimeter of a triangle is 54 inches. If each side has the same length, find the length of a side.
- Let
- The length of a side is
inches.
The length of a side is 18 inches.
Got questions? Get instant answers now!
Sample set c
Six percent of a number is 54. What is the number?
Got questions? Get instant answers now!
Practice set c
Sample set d
An astronomer notices that one star gives off about
times as much energy as another star. Together the stars give off
units of energy. How many units of energy does each star emit?
- In this problem we have two unknowns and, therefore, we might think, two variables. However, notice that the energy given off by one star is given in terms of the other star. So, rather than introducing two variables, we introduce only one. The other unknown(s) is expressed in terms of this one. (We might call this quantity the base quantity.)
Let
number of units of energy given off by the less energetic star. Then,
number of units of energy given off by the more energetic star.
Got questions? Get instant answers now!