5.2 Double integrals over general regions  (Page 5/12)

Finding the area of a rectangular region is easy, but finding the area of a nonrectangular region is not so easy. As we have seen, we can use double integrals to find a rectangular area. As a matter of fact, this comes in very handy for finding the area of a general nonrectangular region, as stated in the next definition.

We have already seen how to find areas in terms of single integration. Here we are seeing another way of finding areas by using double integrals, which can be very useful, as we will see in the later sections of this chapter.

Finding the area of a region

Find the area of the region bounded below by the curve $y=x^2$ and above by the line $y=2x$ in the first quadrant ( [link] ).

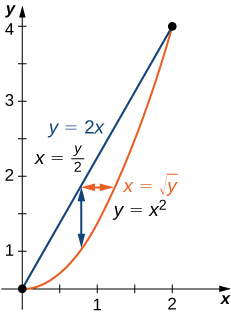
We just have to integrate the constant function $f\left(x,y\right)=1$ over the region. Thus, the area $A$ of the bounded region is ${\displaystyle \underset{x=0}{\overset{x=2}{\int }}{\displaystyle \underset{y=x^2}{\overset{y=2x}{\int }}dydx}}$ or ${\displaystyle \underset{y=0}{\overset{x=4}{\int }}{\displaystyle \underset{x=y\text{/}2}{\overset{x=\sqrt{y}}{\int }}dxdy}}\text{:}$

$A={\displaystyle \underset{D}{\iint }1dxdy={\displaystyle \underset{x=0}{\overset{x=2}{\int }}{\displaystyle \underset{y=x^2}{\overset{y=2x}{\int }}1dydx=}}}{\displaystyle \underset{x=0}{\overset{x=2}{\int }}\left[{y|}_{y=x^2}^{y=2x}\right]}dx={\displaystyle \underset{x=0}{\overset{x=2}{\int }}\left(2x-x^2\right)}dx={x^2-\frac{x^3}{3}|}_0^2=\frac{4}{3}.$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

We can also use a double integral to find the average value of a function over a general region. The definition is a direct extension of the earlier formula.

Finding an average value

Find the average value of the function $f\left(x,y\right)=7x{y}^2$ on the region bounded by the line $x=y$ and the curve $x=\sqrt{y}$ ( [link] ).

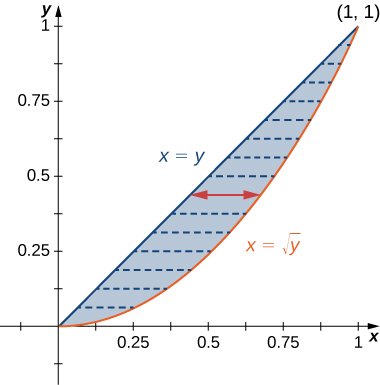
First find the area $A\left(D\right)$ where the region $D$ is given by the figure. We have

$A\left(D\right)={\displaystyle \underset{D}{\iint }1dA={\displaystyle \underset{y=0}{\overset{y=1}{\int }}{\displaystyle \underset{x=y}{\overset{x=\sqrt{y}}{\int }}1dxdy={\displaystyle \underset{y=0}{\overset{y=1}{\int }}\left[{x|}_{x=y}^{x=\sqrt{y}}\right]}}}}dy={\displaystyle \underset{y=0}{\overset{y=1}{\int }}\left(\sqrt{y}-y\right)dy=\frac{2}{3}}{y}^{3\text{/}2}-{\frac{y^2}{2}|}_0^1=\frac{1}{6}.$

Then the average value of the given function over this region is

$\begin{array}{cc}\hfill f_{ave}& =\frac{1}{A\left(D\right)}{\displaystyle \underset{D}{\iint }f\left(x,y\right)dA=\frac{1}{A\left(D\right)}{\displaystyle \underset{y=0}{\overset{y=1}{\int }}{\displaystyle \underset{x=y}{\overset{x=\sqrt{y}}{\int }}7x{y}^{2}dxdy=\frac{1}{1\text{/}6}{\displaystyle \underset{y=0}{\overset{y=1}{\int }}\left[{\frac{7}{2}{x}^2{y}^2|}_{x=y}^{x=\sqrt{y}}\right]}}}}dy\hfill \\ & =6{\displaystyle \underset{y=0}{\overset{y=1}{\int }}\left[\frac{7}{2}{y}^2\left(y-y^2\right)\right]dy=6{\displaystyle \underset{y=0}{\overset{y=1}{\int }}\left[\frac{7}{2}\left(y^3-y^4\right)\right]dy}=\frac{42}{2}}{\left(\frac{y^4}{4}-\frac{y^5}{5}\right)|}_0^1=\frac{42}{40}=\frac{21}{20}.\hfill \end{array}$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Improper double integrals

An improper double integral    is an integral ${\displaystyle \underset{D}{\iint }fdA}$ where either $D$ is an unbounded region or $f$ is an unbounded function. For example, $D=\left\{\left(x,y\right)|\left|x-y\right|\ge 2\right\}$ is an unbounded region, and the function $f\left(x,y\right)=1\text{/}\left(1-x^2-2y^2\right)$ over the ellipse $x^2+3y^2\le 1$ is an unbounded function. Hence, both of the following integrals are improper integrals:

1. ${\displaystyle \underset{D}{\iint }xydA}$ where $D=\left\{\left(x,y\right)|\left|x-y\right|\ge 2\right\};$
2. ${\displaystyle \underset{D}{\iint }\frac{1}{1-x^2-2y^2}dA}$ where $D=\left\{\left(x,y\right)|x^2+3y^2\le 1\right\}.$

In this section we would like to deal with improper integrals of functions over rectangles or simple regions such that $f$ has only finitely many discontinuities. Not all such improper integrals can be evaluated; however, a form of Fubini’s theorem does apply for some types of improper integrals.