| << Chapter < Page | Chapter >> Page > |
Show that does not exist. The graph of is shown here:
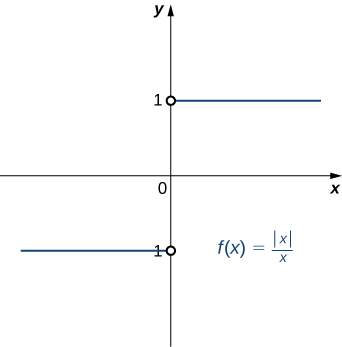
Suppose that L is a candidate for a limit. Choose
Let Either or If then let Thus,
and
On the other hand, if then let Thus,
and
Thus, for any value of L ,
Just as we first gained an intuitive understanding of limits and then moved on to a more rigorous definition of a limit, we now revisit one-sided limits. To do this, we modify the epsilon-delta definition of a limit to give formal epsilon-delta definitions for limits from the right and left at a point. These definitions only require slight modifications from the definition of the limit. In the definition of the limit from the right, the inequality replaces which ensures that we only consider values of x that are greater than (to the right of) a . Similarly, in the definition of the limit from the left, the inequality replaces which ensures that we only consider values of x that are less than (to the left of) a .
Limit from the Right: Let be defined over an open interval of the form where Then,
if for every there exists a such that if then
Limit from the Left: Let be defined over an open interval of the form where Then,
if for every there exists a such that if then
Prove that
Let
Choose Since we ultimately want we manipulate this inequality to get or, equivalently, making a clear choice. We may also determine geometrically, as shown in [link] .
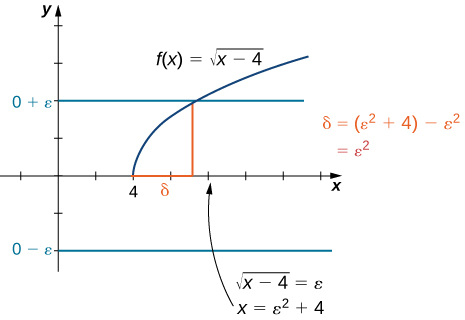
Assume Thus, Hence, Finally,
Therefore,
We conclude the process of converting our intuitive ideas of various types of limits to rigorous formal definitions by pursuing a formal definition of infinite limits. To have we want the values of the function to get larger and larger as x approaches a . Instead of the requirement that for arbitrarily small ε when for small enough we want for arbitrarily large positive M when for small enough [link] illustrates this idea by showing the value of for successively larger values of M .
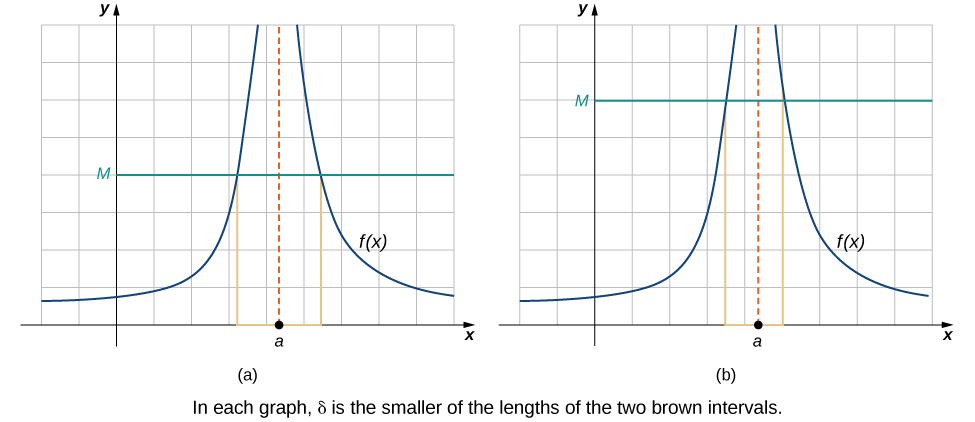
Let be defined for all in an open interval containing a . Then, we have an infinite limit
if for every there exists such that if then
Let be defined for all in an open interval containing a . Then, we have a negative infinite limit
if for every there exists such that if then

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?