Key concepts
- The limit laws allow us to evaluate limits of functions without having to go through step-by-step processes each time.
- For polynomials and rational functions,
- You can evaluate the limit of a function by factoring and canceling, by multiplying by a conjugate, or by simplifying a complex fraction.
- The squeeze theorem allows you to find the limit of a function if the function is always greater than one function and less than another function with limits that are known.
Key equations
-
Basic Limit Results
-
Important Limits
In the following exercises, use the limit laws to evaluate each limit. Justify each step by indicating the appropriate limit law(s).
Use constant multiple law and difference law:
Got questions? Get instant answers now!
In the following exercises, use direct substitution to evaluate each limit.
In the following exercises, use direct substitution to show that each limit leads to the indeterminate form
Then, evaluate the limit.
then,
Got questions? Get instant answers now!
then,
Got questions? Get instant answers now!
In the following exercises, use direct substitution to obtain an undefined expression. Then, use the method of
[link] to simplify the function to help determine the limit.
In the following exercises, assume that
and
Use these three facts and the limit laws to evaluate each limit.
[T] In the following exercises, use a calculator to draw the graph of each piecewise-defined function and study the graph to evaluate the given limits.
In the following exercises, use the following graphs and the limit laws to evaluate each limit.
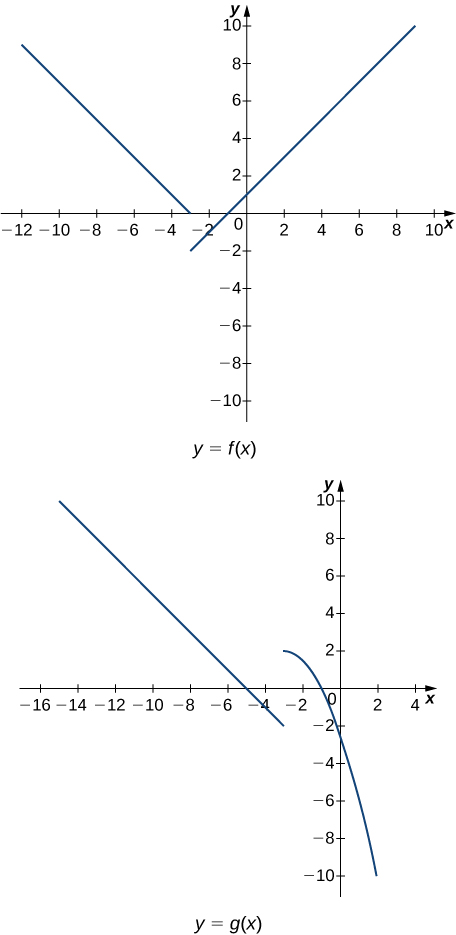
Got questions? Get instant answers now!
For the following problems, evaluate the limit using the squeeze theorem. Use a calculator to graph the functions
and
when possible.
[T] In physics, the magnitude of an electric field generated by a point charge at a distance
r in vacuum is governed by Coulomb’s law:
where
E represents the magnitude of the electric field,
q is the charge of the particle,
r is the distance between the particle and where the strength of the field is measured, and
is Coulomb’s constant:
- Use a graphing calculator to graph
given that the charge of the particle is
- Evaluate
What is the physical meaning of this quantity? Is it physically relevant? Why are you evaluating from the right?
a.
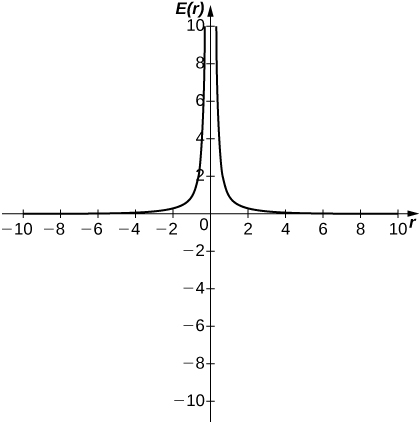
b. ∞. The magnitude of the electric field as you approach the particle
q becomes infinite. It does not make physical sense to evaluate negative distance.
Got questions? Get instant answers now!
[T] The density of an object is given by its mass divided by its volume:
- Use a calculator to plot the volume as a function of density
assuming you are examining something of mass 8 kg (
- Evaluate
and explain the physical meaning.
Got questions? Get instant answers now!


